|
Un approfondimento "giocoso" sui paesaggi virtuali con gli apporti di (in ordine alfabetico): Gisella Malagodi, Giovanna Maria Melis, Ivana Niccolai, Giorgio Pietrocola e Grazia Raffa
Bibliografia: “PENTOLE, OMBRE, FORMICHE ( In viaggio con la matematica)" di Emma Castelnuovo, ed. La Nuova Italia; "IL
TURISTA MATEMATICO- Un viaggio nella moderna scienza dei numeri",
di Ivars Peterson, Traduzione di Riccardo Valla, Rizzoli, 1991 |
||
|
Un paesaggio virtuale realizzato da Gisella Malagodi
Ode ai paesaggi virtuali (di Grazia Raffa e Ivana Niccolai)
La geometria frattale è proprio eccezionale: un elegante modo per non lavorar sodo,
ma disegnare al vero e senza alcun mistero gli oggetti naturali, sul video-schermo, tali.
Questo semplice sistema è chiaro che non trema: permette di costruire montagne a non finire
e, ciò che è costruito, dal triangolo è partito. Il punto (di ogni lato) ch'è medio va fissato;
da questi medi punti, si traggono gli spunti: così un segmento tale, in linea verticale,
sul lato si costruisce, quale polla scaturisce e il "verticale/lato" ora viene "dimezzato";
scegliendo diversamente, va bene tutto ugualmente. Un caso consideriamo: segmenti dividiamo:
poi, con la verticale, unirli è magistrale. Sui lati "nuovi" procedi e una meraviglia vedi;
ripeti la costruzione, capirai la soluzione! La regola permette di erigere le vette,
variando a ogni tappa l'aspetto della mappa, cambiando il rapporto senza trovarsi in torto:
segmento in verticale e il lato suo basale. Si è liberi, pertanto, di erigere quel tanto,
fissandone il valore, come ci dice il cuore: i triangoli saranno costruiti come vanno
e ripidi più o meno qual triangolo scaleno. Dopo ripetizioni, secondo le opinioni,
di "verticale/lato" del tipo più variato, si forma una montagna: è una vera cuccagna.
Segmenti verticali possono essere tali, in quanto han facoltà che in basso porterà.
Con queste linee "tronche", vedremo valli e conche; con il calcolatore avremo anche il colore.
Scenografi eccellenti, ben ricchi di talenti, adoperan paesaggi intorno ai personaggi,
nei luoghi più incredibili gli stessi son visibili: su schermo "ammazza-ore" di un buon calcolatore.
Qualcuno già si chiede, di certo in buona fede: quanto qui programmato è come un quadro nato
da artista col pennello, anche se non è quello? Si può parlar di arte, come giocando a carte?
Se un Giovanni Bellini, con tinte e pennellini, tornasse a lavorare, avrebbe da imparare...
La matematica è arte, la si loda d'ogni parte! La frattale geometria siam ben lieti che ci sia.
E' stata da noi analizzata anche un'altra procedura per la costruzione di una montagna; cliccare qua
|
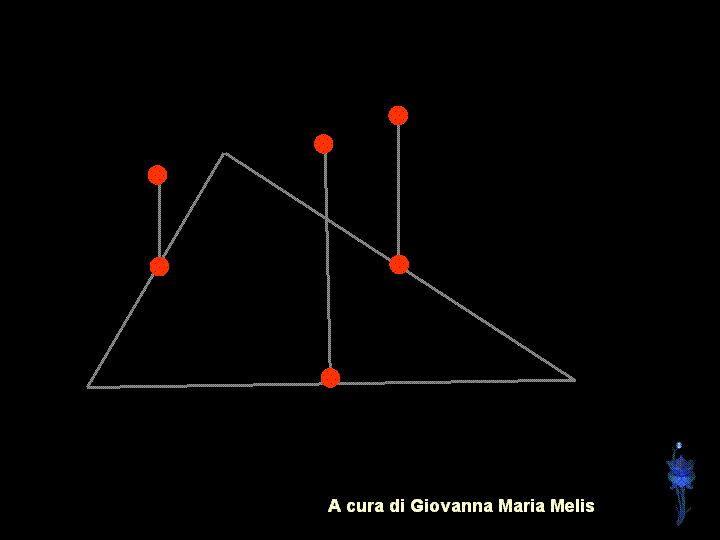
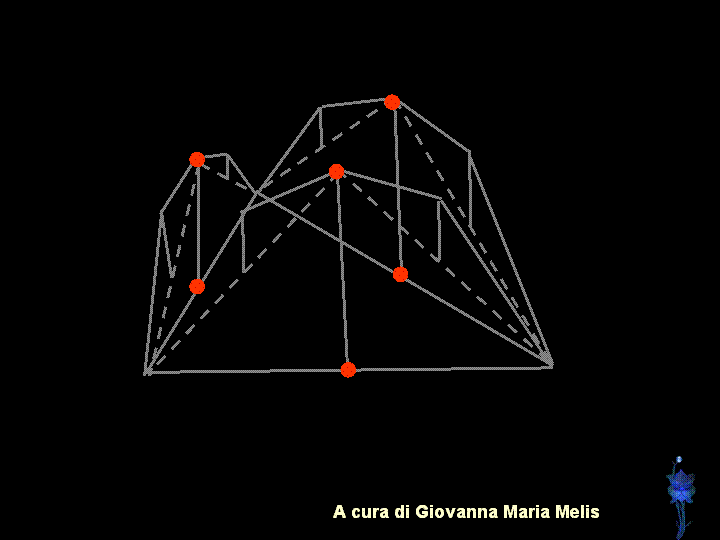
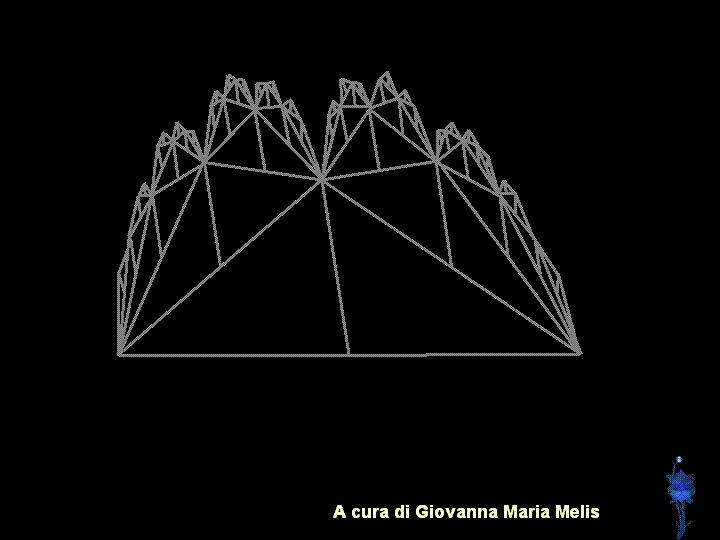
Un esempio dei possibili passaggi
grafici per la costruzione di una montagna, a cura di Giovanna Maria
Melis:
Per visionare alcune animazioni particolarmente significative, realizzate da Giorgio Pietrocola, cliccare qui
Per leggere le istruzioni per l'uso di Terragen, un programma specifico per generare paesaggi, scritte da Gisella Malagodi, cliccare qua Un altro paesaggio virtuale realizzato da Gisella Malagodi
|
|