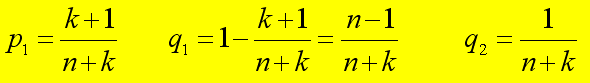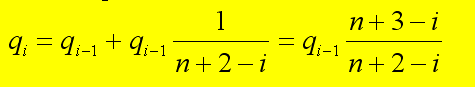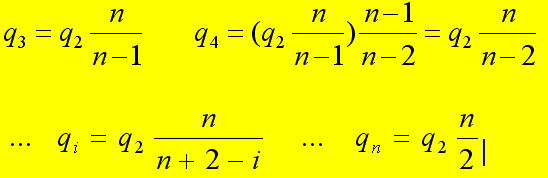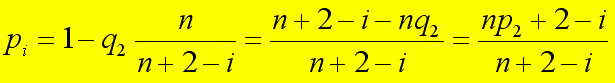|
La risoluzione del
problema "Il volo intercontinentale" è il frutto di
una collaborazione tra colleghi e amici virtuali, nata nel forum A
dell'Indire, (dove il moderatore UMI, Fabio Brunelli, ha RIPORTATO tale
"quesito" GIA'
PROPOSTO DA MICHELE IMPEDOVO, inerente alla probabilità) e proseguita "altrove",
tramite la posta
elettronica, che ha consentito lo scambio di una proficua messaggistica
privata, in cui sono stati coinvolti principalmente Flavio Cimolin, Dino
Liberatore, Giorgio Pietrocola e la sottoscritta, per approfondire
determinati aspetti e per giungere a una "generalizzazione" condivisa.
Reputo DOVEROSO RINGRAZIARE Claudio Rosanova, sempre infaticabilmente
disponibile ad accogliere nel sito di maecla i contributi dei colleghi,
Fabio Brunelli, Flavio Cimolin, Nicola Santoro, disposti al dialogo e al
confronto, ma SOPRATTUTTO DINO LIBERATORE e GIORGIO PIETROCOLA (nominati
esclusivamente in ordine alfabetico!), che hanno messo a disposizione una
competenza e una motivazione ammirevoli, per continuare ad alimentare
insieme la loro inesauribile "curiosità cognitiva", dimostrandosi pronti
al lavoro più impegnativo, per sistematizzare i risultati
raggiunti, raccogliendoli in un unico file, da loro preparato. La matematica è
servita, così, per stimolare la comunicazione e la
cooperazione intorno al "dibattito" su un problema interessante, cercando
di comprendere i diversi procedimenti seguiti e i modi personali di
affrontare un quesito "non banale", per pervenire alla necessaria
dimostrazione. Si è passati dall'intuizione al rigore, in quanto si è giunti
alla
successiva sistematizzazione formale delle varie riflessioni, a priori
esplicitate e condivise con differenti modalità.
Ringrazio ancora tutti, per la splendida esperienza vissuta.
Ivana Niccolai
Volo
intercontinentale
I 300 passeggeri di un volo intercontinentale salgono in
cabina nello stesso ordine del numero di posto assegnato. Il primo passeggero è,
in realtà, uno sprovveduto in quanto non sa di doversi sedere al posto al posto
numero uno e così si accomoda in un posto a caso. Tutti gli altri passeggeri
invece si siedono al loro posto, sempre che questo risulti libero, altrimenti
scelgono un posto a caso tra quelli rimasti ancora liberi.
Qual è la probabilità che il trecentesimo passeggero si sieda
al posto assegnatoli e cioè al numero 300?
Soluzione
Per rispondere alla domanda posta possiamo procedere
secondo un ragionamento puramente logico: infatti, con riferimento al testo
del problema, sappiamo che il primo passeggero si siederà a caso su uno dei
300 posti disponibili; se si è seduto al posto contraddistinto col numero due
il secondo passeggero si siederà ad un altro posto, altrimenti si siederà al
suo posto. A questo punto poco importa chi ci sia seduto lì, il posto numero
due sarà sicuramente occupato. La stessa situazione si verifica dopo che è
entrato anche il terzo passeggero: il posto numero tre sarà certamente
occupato. Arrivati al passeggero 299-esimo la situazione è sempre la stessa:
tutti i posti dal due al 299 saranno certamente occupati. Resterà quindi
libero o il posto numero uno od il posto numero 300. Ma sono equiprobabili
questi due eventi? Certamente sì! Il tutto dipende, infatti, dal primo
passeggero: se si è seduto al suo posto anche tutti gli altri andranno al loro
posto ed alla fine resterà libero il posto numero 300; altrettanto se si è
seduto al posto numero 300, ma in tal caso alla fine resterà libero il primo
posto che andrà ad essere occupato dall’ultimo passeggero; mentre invece se si
è seduto su un posto tra il due ed il 299, prima o poi qualcuno andrà ad
occupare il primo posto od il 300-esimo con probabilità che sono chiaramente
uguali. In conclusione l’ultimo passeggero ha il 50 % di probabilità di
trovare il suo posto libero.
(Dimostrazione curata da Paolo Bonavoglia.)
Come si vede questa dimostrazione, contrariamente a quella
matematica che faremo tra breve, salta a piè pari tutte le persone che vanno
dalla seconda alla 299-esima e giunge rapidamente al risultato richiesto. Per la
dimostrazione matematica partiamo per gradi e consideriamo dapprima il caso che
ci siano solamente due passeggeri a salire sull’aereo per poi generalizzare ad n
passeggeri. In tal caso l’ultimo passeggero, e cioè il secondo, si siederà al
suo posto solamente se il primo si siederà al proprio, cioè con una probabilità
pari ad 1/2 ossia del 50 %.
Per tre passeggeri rivoltiamo la domanda e determiniamo qual
è la probabilità che l’ultimo arrivato, il terzo passeggero, non si sieda al suo
posto. Sicuramente questo accade se il primo passeggero si siede al posto numero
tre, evento che ha probabilità pari ad 1/3, ma può accadere anche se il primo si
siede al posto numero due e poi il secondo si siede casualmente al posto numero
tre, evento che ha probabilità 1/3·1/2 = 1/6. Quindi la probabilità totale che
il terzo non si sieda al proprio posto è data da:
1/3 + 1/6 = (2 + 1)/6 = 3/6 = 1/2
Dunque anche in questo caso l’ultimo passeggero ha una
probabilità su due di sedersi al proprio posto.
Continuando il ragionamento nello stesso modo, ci chiediamo
qual è la probabilità che, su quattro passeggeri, il quarto non si sieda al
posto numero quattro. La cosa può accadere per uno dei seguenti quattro motivi:
a) Se il primo passeggero si siede al posto numero quattro con probabilità 1/4;
b) Se il primo passeggero si siede al posto numero tre ed il terzo si siede al
numero quattro con probabilità 1/4·1/2 = 1/8;
c) Se il primo passeggero si siede al posto numero due ed il secondo si siede al
numero quattro con probabilità 1/4·1/3 = 1/12;
d) Se il primo passeggero si siede al posto numero due, il secondo si siede al
numero tre ed il terzo si siede al numero quattro con probabilità 1/4·1/3·1/2 =
1/24.
Il totale della probabilità che l’ultimo passeggero non si sieda al suo posto è
allora pari a:
1/4 + 1/8 + 1/12 + 1/24 = (6 + 3 + 2 + 1)/24 = 12/24 = 1/2
Dunque anche per quattro passeggeri la probabilità che
l’ultimo si sieda al proprio posto è ancora del 50 %.
Proviamo allora, alla luce di questi esempi, ad effettuare la
generalizzazione al caso di n passeggeri, calcolando sempre la probabilità che
l’ennesimo passeggero non si sieda al proprio posto. Vedremo che per induzione
tale probabilità resta sempre costante e uguale a 1/2. Cercheremo di dimostrarlo
riconducendoci ai casi già visti. Chiamiamo allora con p(n) la probabilità che
con n passeggeri l’ultimo non si sieda al proprio posto. Abbiamo finora
determinato che risulta:
p(2) = p(3) = p(4) = 1/2
Dunque ora, per n maggiore di quattro, effettuiamo il
ragionamento seguente: la probabilità che l’ultimo passeggero non si sieda al
proprio posto dipende dalla scelta del primo passeggero nel seguente modo:
a) Se egli si siede al posto numero uno, cioè il proprio posto, allora tutti si
siederanno al proprio posto, e dunque anche l’ultimo farà lo stesso;
b) Se egli si siede al posto numero due, allora quello che accade
successivamente è esattamente lo stesso problema che si avrebbe con n - 1
passeggeri; basta pensare, infatti, al secondo passeggero, che si siede a caso
perché ha il posto occupato, come al primo di un problema con n - 1 anziché n
passeggeri. Dunque la probabilità che l’ultimo non si sieda al proprio posto se
il primo si siede al posto numero due equivale a p(n - 1);
c) Se egli si siede al posto numero tre, allora il secondo si siederà al proprio
posto, e, per il terzo passeggero, potremo ragionare di nuovo come fatto nel
caso precedente: la probabilità che l’ultimo non si sieda al proprio posto, se
il primo si siede al posto numero tre, equivale esattamente alla probabilità che
si verificherebbe nel caso ci fossero solo n - 2 passeggeri ovvero alla p(n -
2);
d) Continuando lo stesso ragionamento, se egli si siede al posto numero quattro,
allora la probabilità che l’ultimo non si sieda al proprio posto equivale a p(n
- 3);
.....................................................................................................................................................
n) Se il primo si siede al posto n, allora sicuramente l’ultimo non si siederà
al proprio posto, dunque in questo caso la probabilità è proprio unitaria e
quindi certa.
Riepilogando tutti i possibili casi precedenti, in formule si ha:
p(n) = (1/n)·p(n - 1) + (1/n)·p(n - 2) + (1/n)·p(n - 3) + ...
+ (1/n)·p(3) + (1/n)·p(2) + (1/n)·1 =
= (1/n)·[1 +p(2) + p(3) + ... + p(n - 3) + p(n - 2) + p(n - 1)]
Ora il ragionamento induttivo ci insegna a dire: supponiamo
che tutti i p(i) siano uguali tra loro e pari ad 1/2 e per i che va da due ad n
- 1, allora dimostriamo che è anche p(n) = 1/2. Ed infatti si ha:
p(n) = (1/n)·[1 + (n - 2)·1/2] = (1/n)·(n/2) = 1/2
E così la dimostrazione è completa: indipendentemente da
quanti passeggeri ci sono, la probabilità che l’ultimo passeggero si sieda al
suo posto è esattamente uguale a quella che non si sieda affatto, cioè sempre
pari al 50 %.
Andiamo a determinare ora anche tutte le probabilità degli
altri passeggeri di sedersi al loro posto: quindi, se questi sono n, il primo
ha probabilità 1/n di sedersi al suo posto; questa però è anche la
probabilità che occupi il posto numero due, per cui quella di lasciarlo libero,
essendo complementare, vale (n - 1)/n. Il secondo passeggero ha perciò la
probabilità di sedersi al suo posto uguale a quella che il primo non lo
occupa e cioè (n - 1)/n. Il terzo passeggero potrà accomodarsi al suo
posto solo se non si è seduto prima di lui il primo od il secondo passeggero; il
primo, come al solito, ha probabilità pari ad 1/n di sedersi a quel posto; anche
il secondo, però, ha probabilità 1/n di trovare il proprio posto occupato ed in
tal caso potrebbe occupare il posto numero tre sugli n - 1 rimasti disponibili
con un’ulteriore probabilità pari a 1/(n - 1) e per una complessiva uguale a
1/[n·(n - 1)]. Quindi il terzo passeggero non si siederà affatto al suo posto
con probabilità:
1/n + 1/[n·(n - 1)] = (n - 1 + 1)/[n·(n - 1)] = n/[n·(n - 1)]
= 1/(n - 1)
ovvero il terzo passeggero si siederà al suo posto con
probabilità pari a:
1 - 1/(n - 1) = (n - 1 - 1)/(n - 1) = (n - 2)/(n - 1)
In modo del tutto analogo si dimostra facilmente che il
quarto passeggero si siederà al suo posto con una probabilità pari a (n - 3)/(n
- 2), il quinto con probabilità (n - 4)/(n - 3), e così via per cui l’i-esimo si
accomoda al suo posto con [n - (i - 1)]/[n - (i - 2)] di probabilità.
Ciò si verifica quindi fino al (n - 2)-iesimo passeggero (il
terz’ultimo) con probabilità:
{n - [(n - 2) - 1]}/{n - [(n - 2) - 2]} = 3/4
al (n - 1)-iesimo (il penultimo) con probabilità:
{n - [(n - 1) - 1]}/{n - [(n - 1) - 2]} = 2/3
e, finalmente, all’ennesimo (l’ultimo) passeggero con
probabilità pari a:
[n - (n - 1)]/[n - (n - 1)] = 1/2
Come si vede, anche con tale ulteriore dimostrazione
matematica, per giungere alla risposta del problema, non occorre calcolare
necessariamente la probabilità di tutti i passeggeri prima di determinare quella
dell’ultimo e né ricorrere all’induzione come visto in precedenza.
|
Una
generalizzazione del problema. (di Giorgio Pietrocola) |
|
n passeggeri di un volo
intercontinentale salgono in cabina nello stesso ordine del numero di posto
assegnato. Il primo passeggero è, in realtà, uno sprovveduto in quanto non sa di
doversi sedere al posto numero uno e così si accomoda in un posto a caso.
Nello scegliere un posto a caso però considera n+k (k>=0) posti e
sorteggia un numero corrispondente. Nei casi in cui esce un numero superiore a n
finisce tra il personale di servizio e viene fatto sedere al suo posto,il numero
uno. Tutti
gli altri passeggeri invece si siedono al loro posto, sempre che questo risulti
libero, altrimenti scelgono un posto a caso tra quelli rimasti ancora liberi. Qual è la probabilità che
l'ultimo passeggero si sieda al posto assegnatoli e cioè al numero n? |
|
Siano P1, P2,
P3, ..., Pi, ..., Pn i vari posti disponibili sull’aereo prima che salgano i viaggiatori
che indicheremo rispettivamente con V1, V2, V3, ..., Vi, ..., Vn.
Chiamiamo ora pi la probabilità che il passeggero Vi si sieda in Pi, cioè al proprio
posto, e qi = 1 - pi la probabilità contraria cioè quella che Vi non si sieda in
Pi. Come abbiamo visto risulta:
infatti delle n alternative di V1, ugualmente possibili, solo il caso che V1 si
metta in P2 costringe V2 a non sedersi al suo posto.
Sappiamo che V1, V2, V3, ..., Vi - 2
possono causare l’occupazione
di Pi - 1 con probabilità qi - 1,
Gli stessi viaggiatori, evidentemente, potranno, causare anche l’occupazione
di Pi, con identica probabilità ma questa potrà essere anche causata dall’occupazione di Pi - 1 nel caso che Vi - 1 , trovato occupato il suo posto, degli n - (i - 2) posti rimasti liberi, scelga proprio
Pi. Deve dunque essere:
Da questa relazione sostituendo si trova:
da cui anche:
|
|
Casi particolari: |
Variante 1 (formulazione originale)
I 300 passeggeri di un volo
intercontinentale salgono in cabina nello stesso ordine del numero di posto
assegnato. Il primo passeggero è, in realtà, uno sprovveduto in quanto non sa di
doversi sedere al posto numero uno e così si accomoda in un posto a caso.
Tutti gli altri passeggeri invece si siedono al loro posto,
sempre che questo risulti libero, altrimenti scelgono un posto a caso tra quelli
rimasti ancora liberi. Qual è la probabilità che il trecentesimo passeggero si
sieda al posto assegnatoli e cioè al numero 300? |
|
Basta porre n=300 i=300 k=0 per ottenere: q2=1/300
p2=299/300 p300=1/2 |
Variante 2
I 300 passeggeri di un volo intercontinentale salgono in cabina nello stesso
ordine del numero di posto assegnato. Il primo passeggero è, in realtà, uno
sprovveduto in quanto non sa di doversi sedere al posto numero uno e così si
accomoda in un posto a caso. Nello scegliere un posto a caso però
considera il doppio dei posti e sorteggia un numero corrispondente. Nei casi in
cui esce un numero superiore a 300 finisce tra il personale di servizio e viene
fatto sedere al suo posto. Tutti gli altri passeggeri invece si siedono
al loro posto, sempre che questo risulti libero, altrimenti scelgono un posto a
caso tra quelli rimasti ancora liberi. Qual è la probabilità che il trecentesimo
passeggero si sieda al posto assegnatoli e cioè al numero 300? |
|
Basta porre n=300 i=300 k=300 per ottenere: q2=1/600
p2=599/600 p300=3/4 |
Torna a MATEMATICA
Torna alla pagina iniziale
|