Plastic rectangle and Padovan sequence

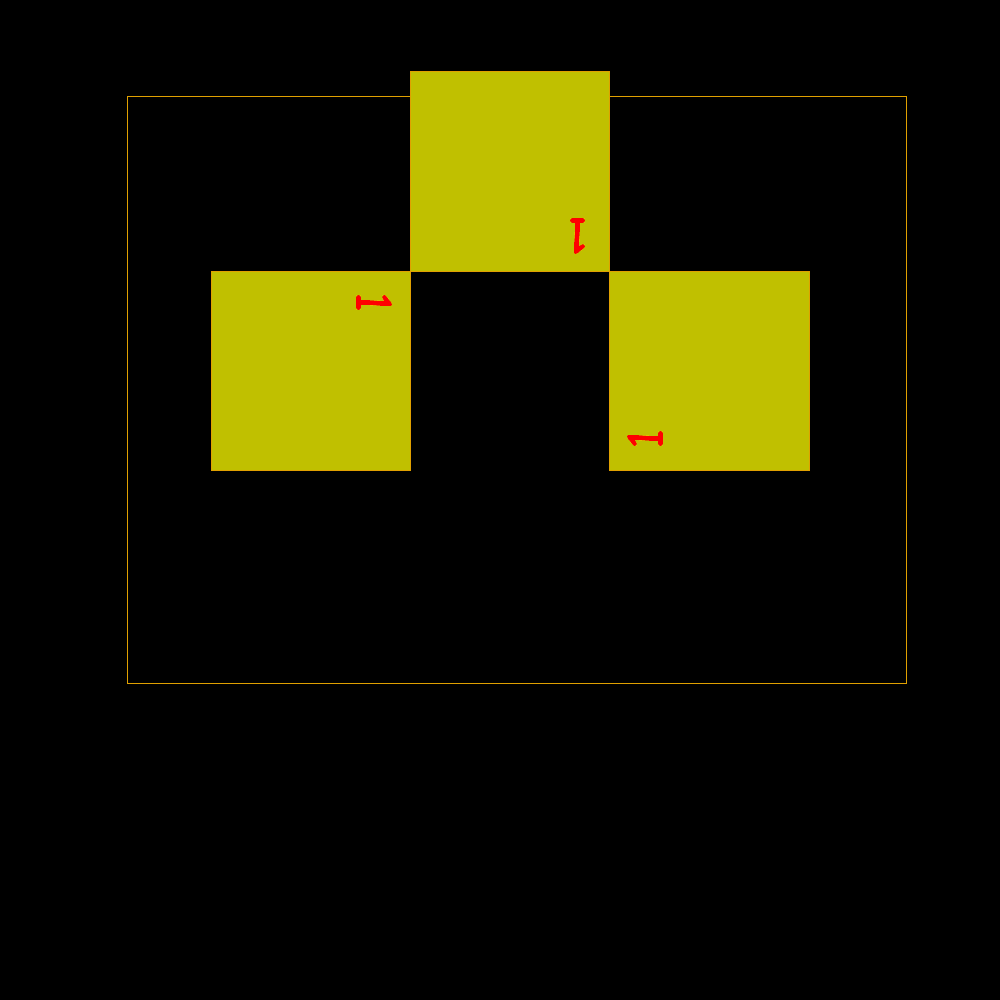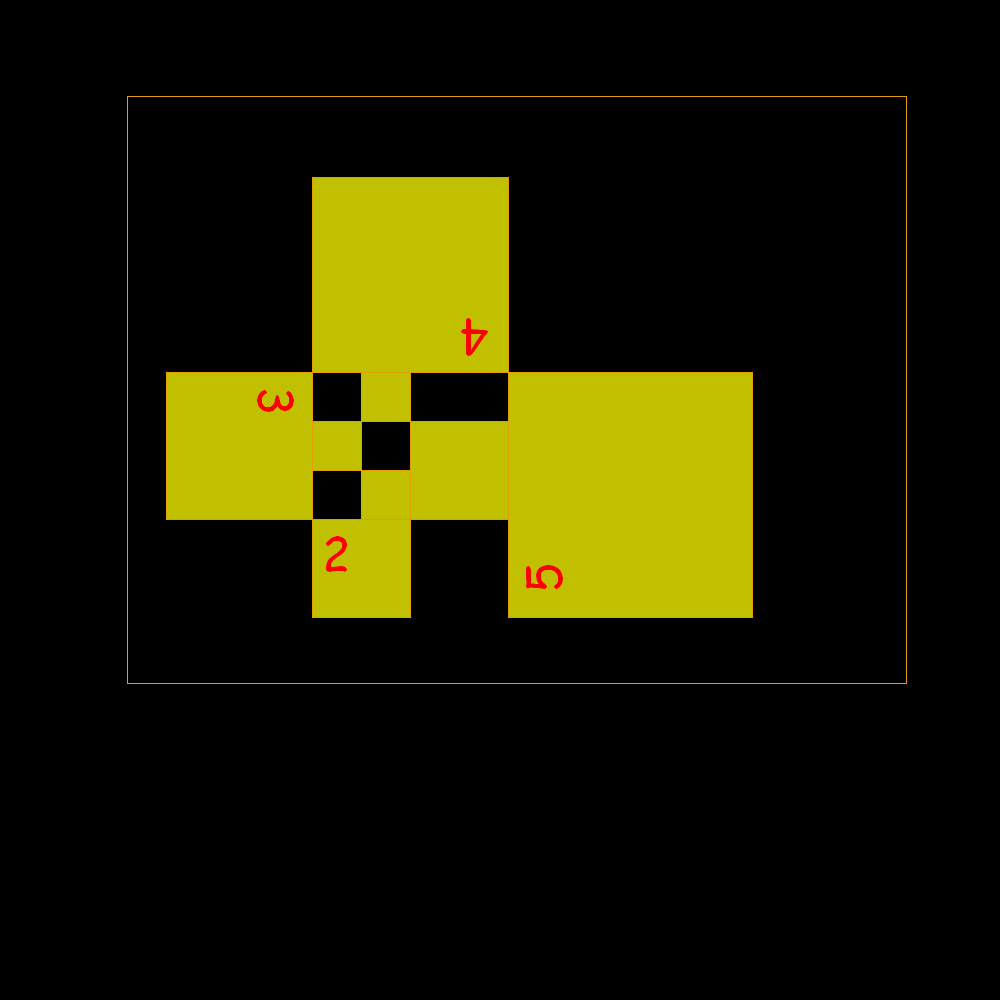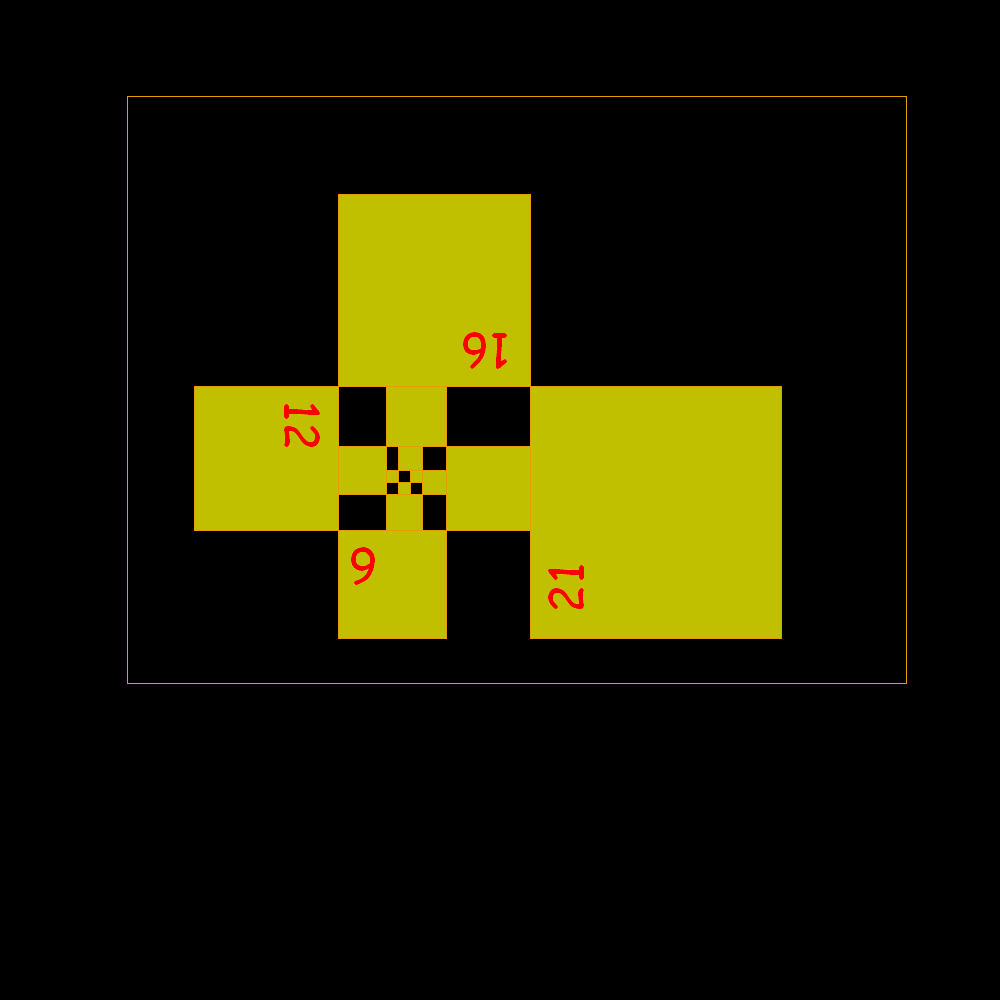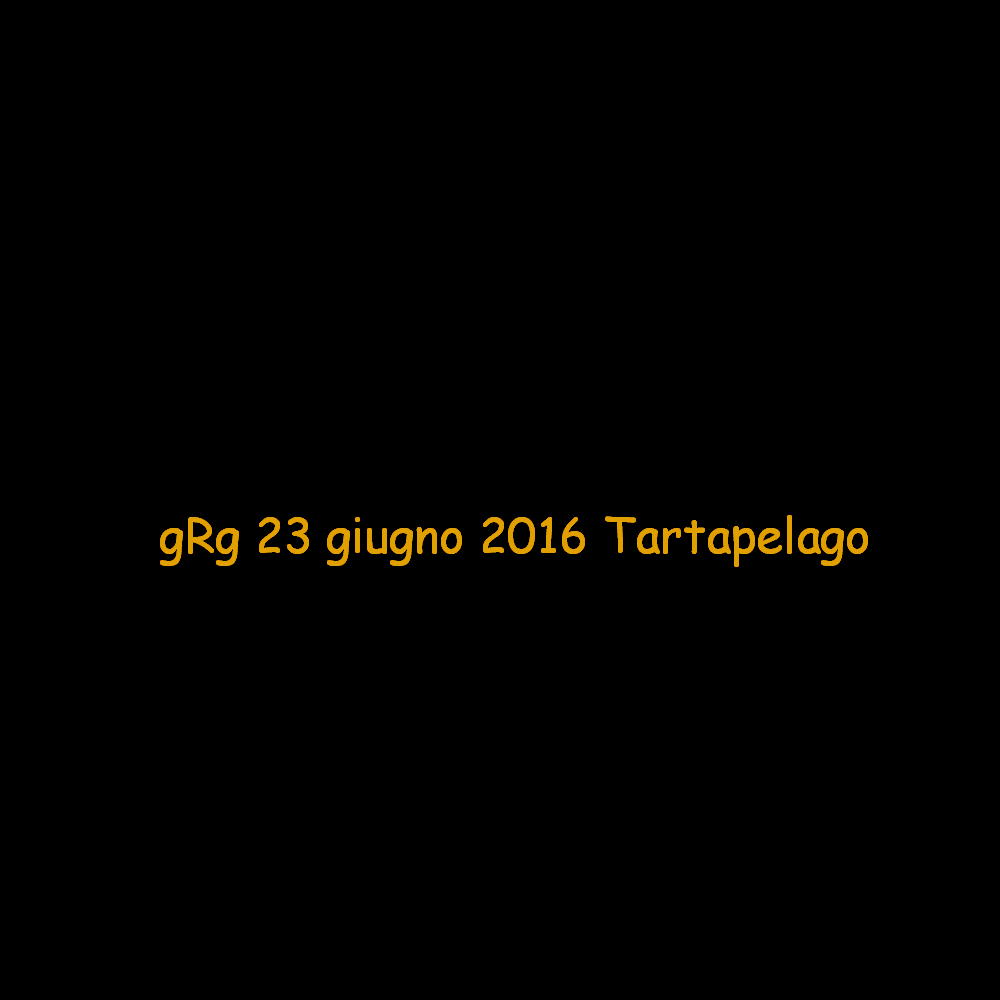
It is observed that the side of a square equals the sum of the two not immediately preceding.
For this you can tend to the plastic rectangle building rectangles with square in the following sequence:

1, 1, 1, 2, 2, 3, 4, 6, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, 465, 616, 816, 1081,...

that it is the famous Padovan numbers


Ratio of two consecutive numbers of the sequence tends to the relationship between major and minor side of the golden rectangle ::

P=1.324717957... plastic number       one of the solutions of the following equation:
r³-r-1=0

(1/P=0.7548776662...one of the solutions of the following equation: r³+r²-1=0)

Start of rectangles identified by square building with sides according to the Padovan sequence

Shortly after the result is confused with the plastic rectangle to which it tends

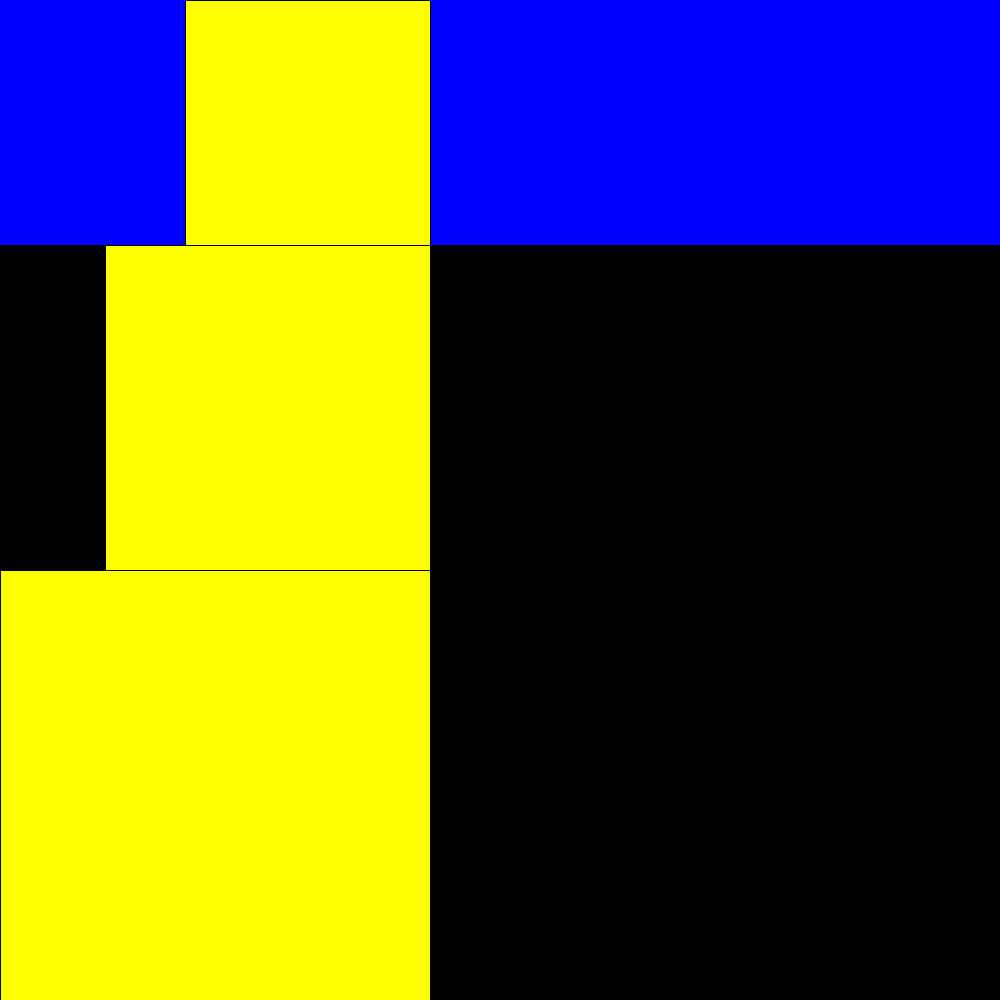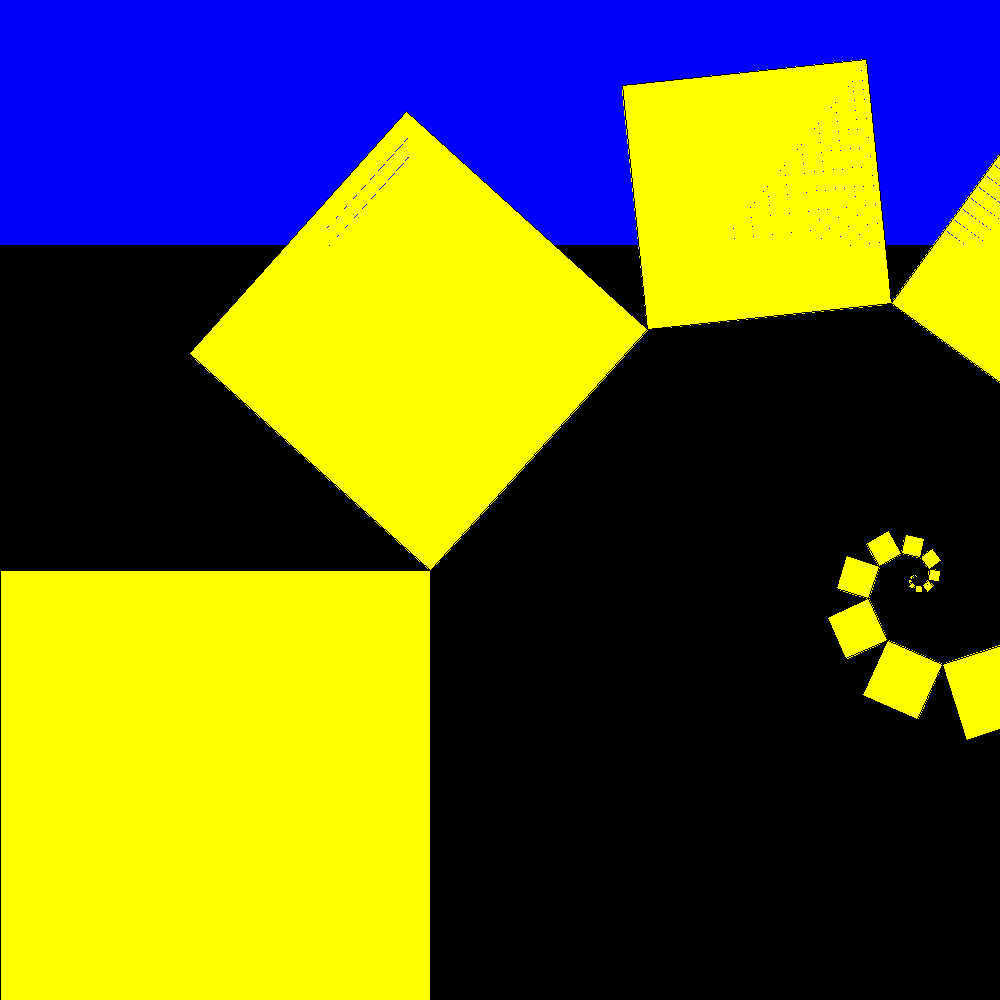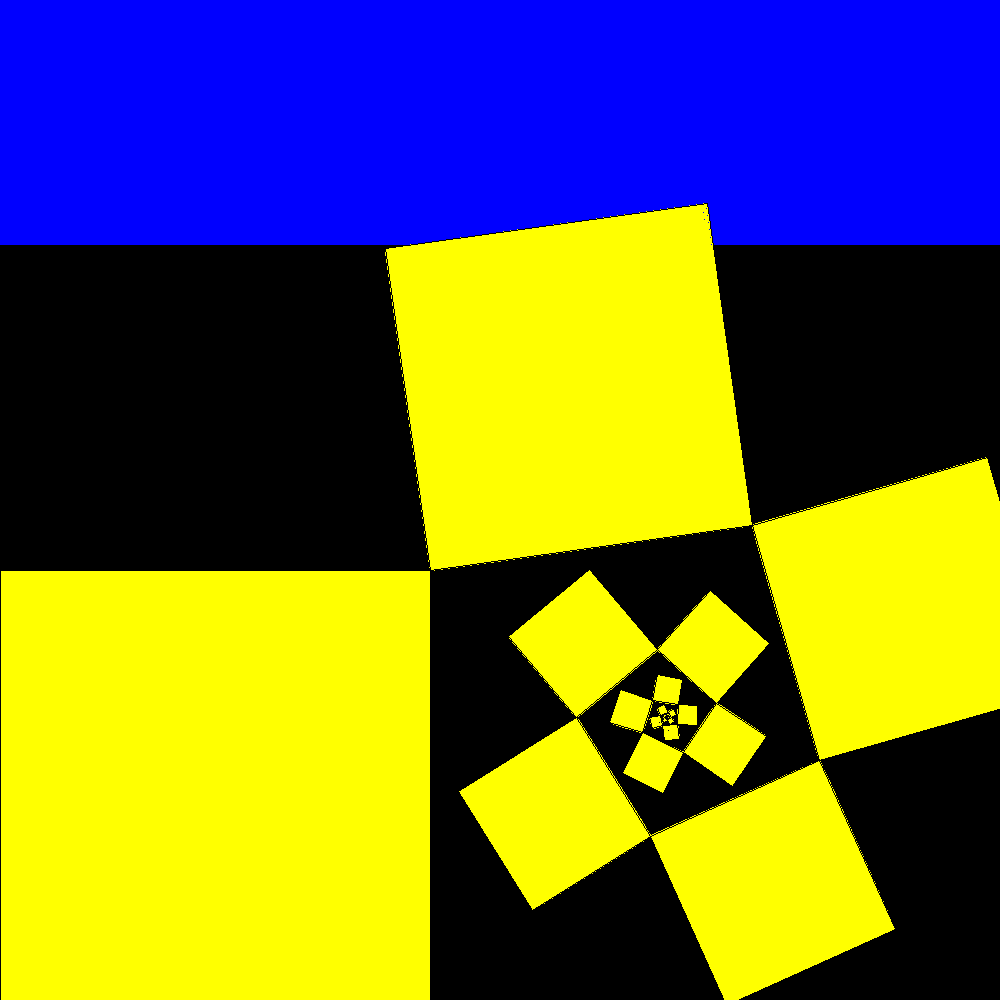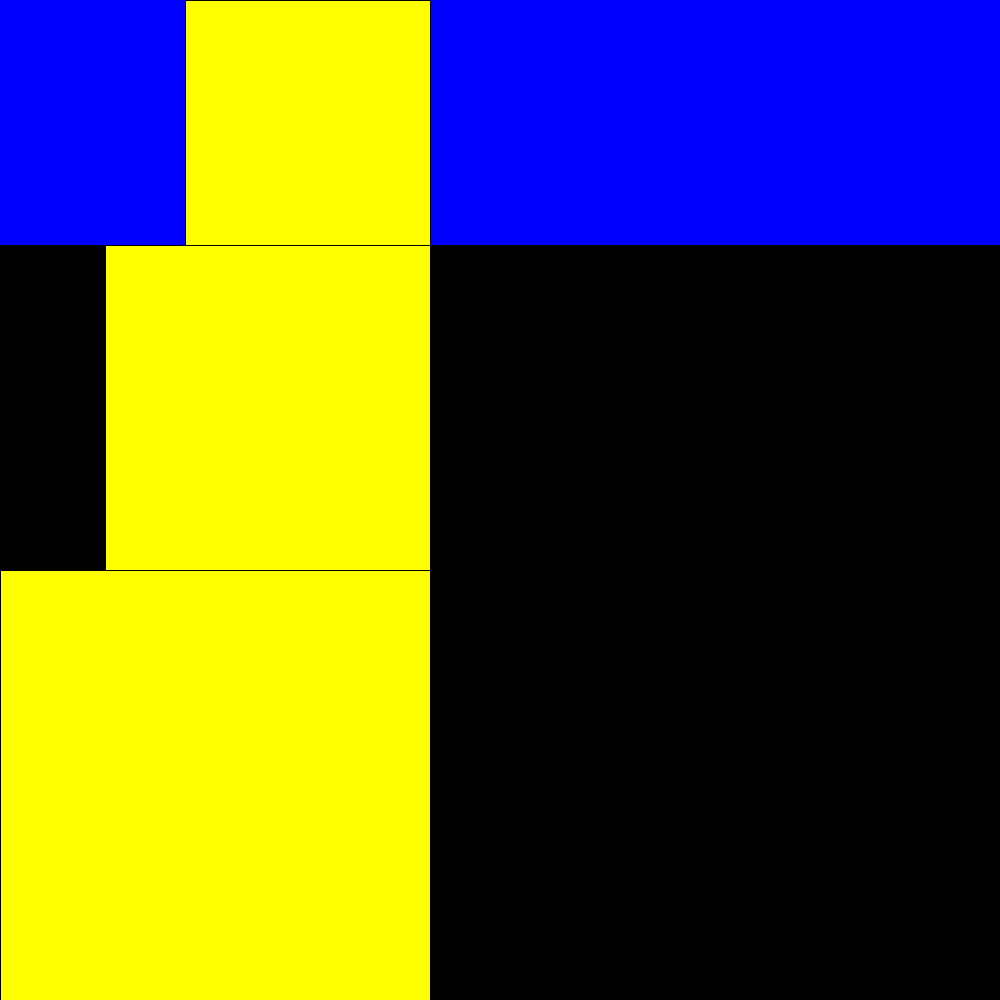packing and unpacking

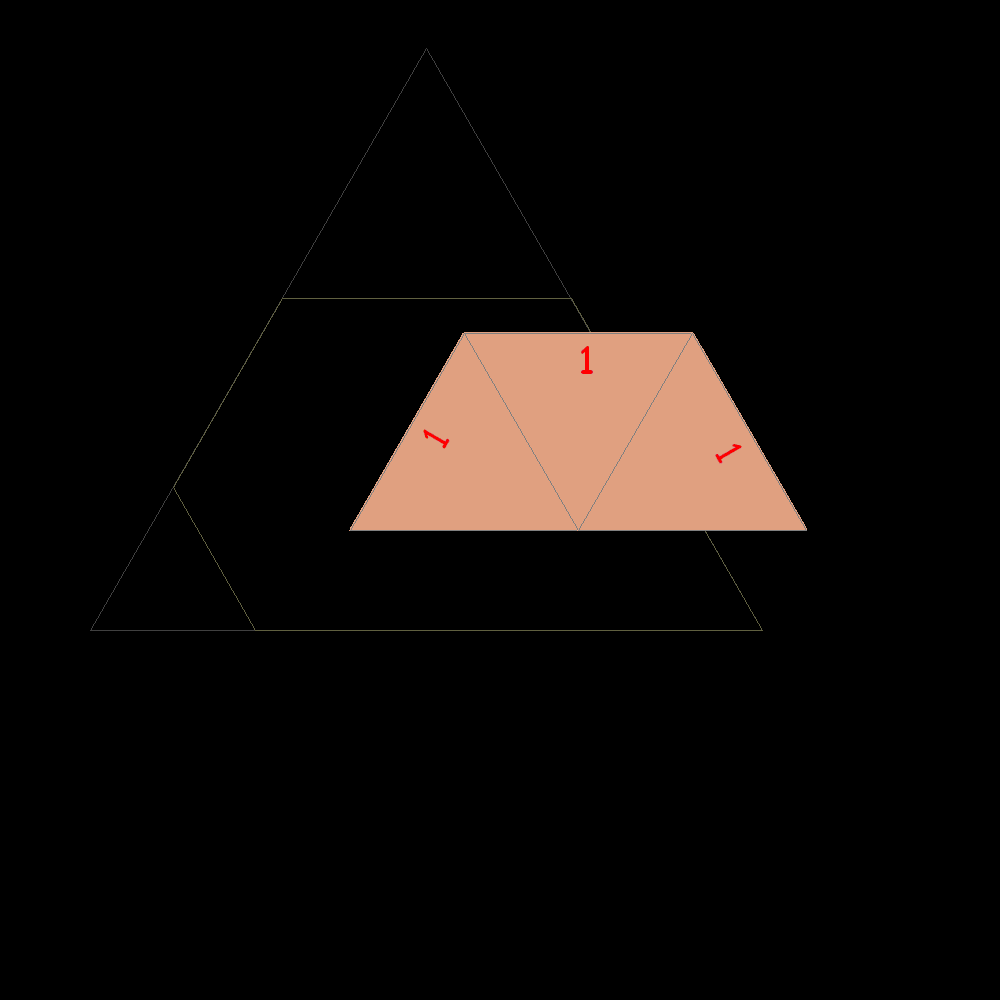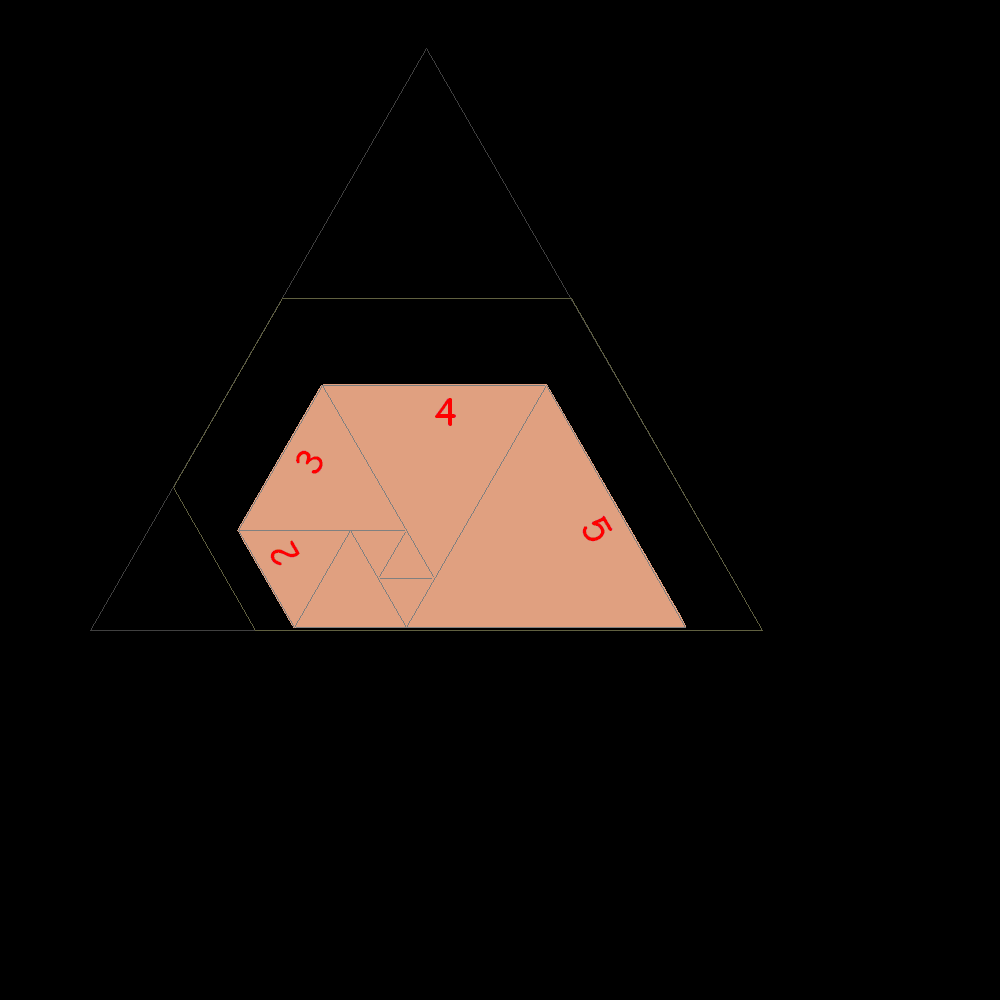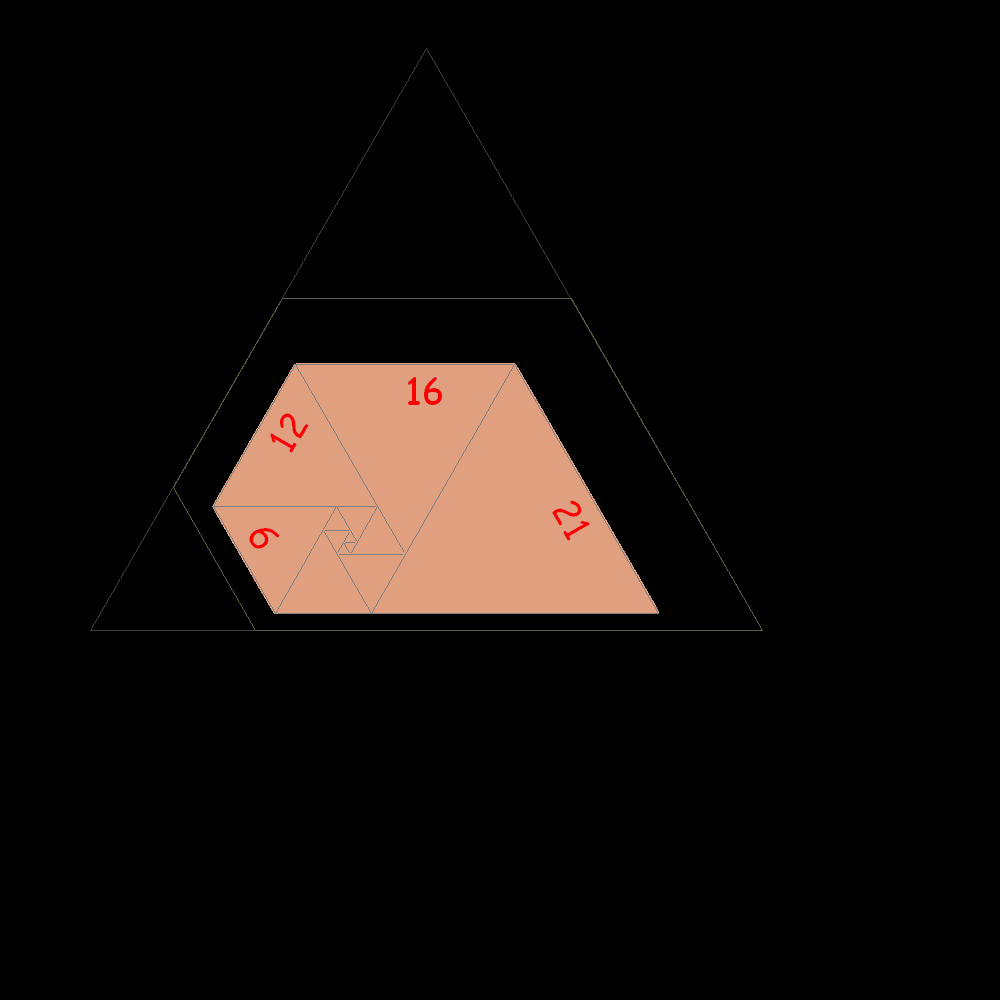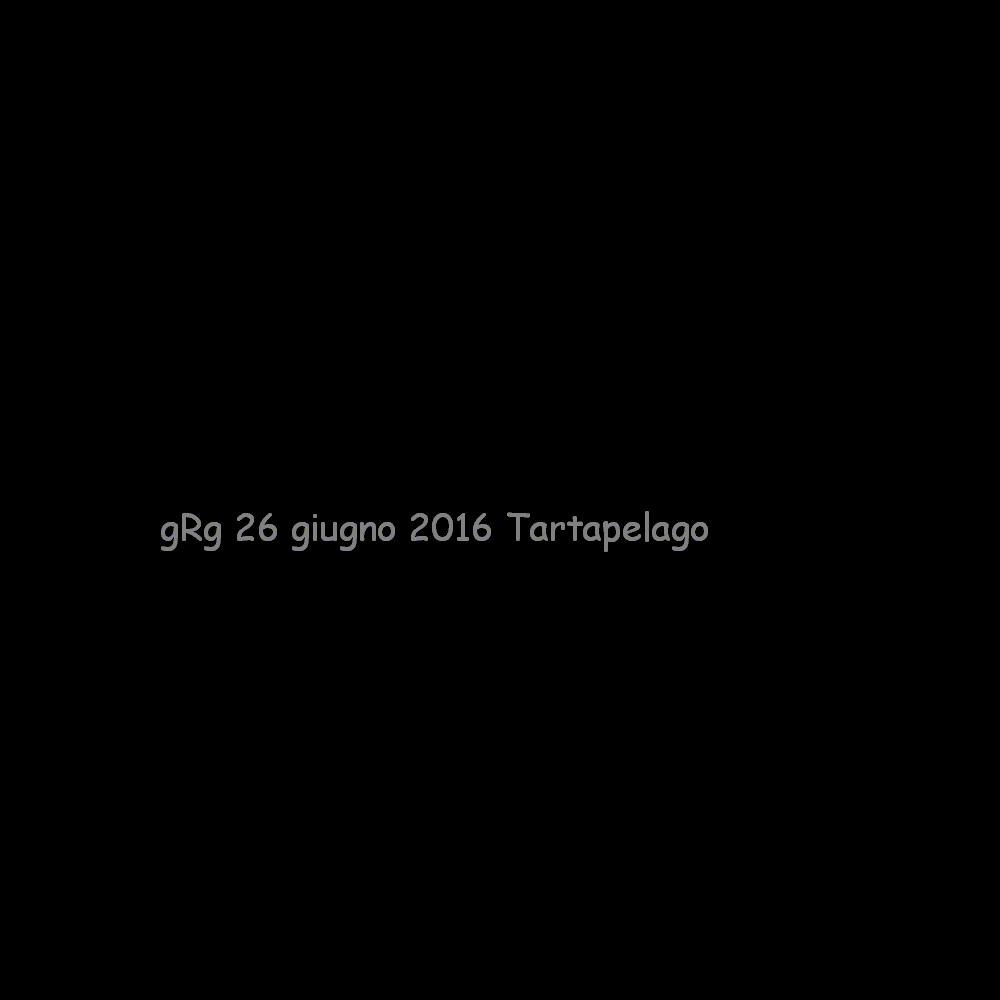
Start of construction of trapezes with equilateral triangles according with the  Padovan sequence

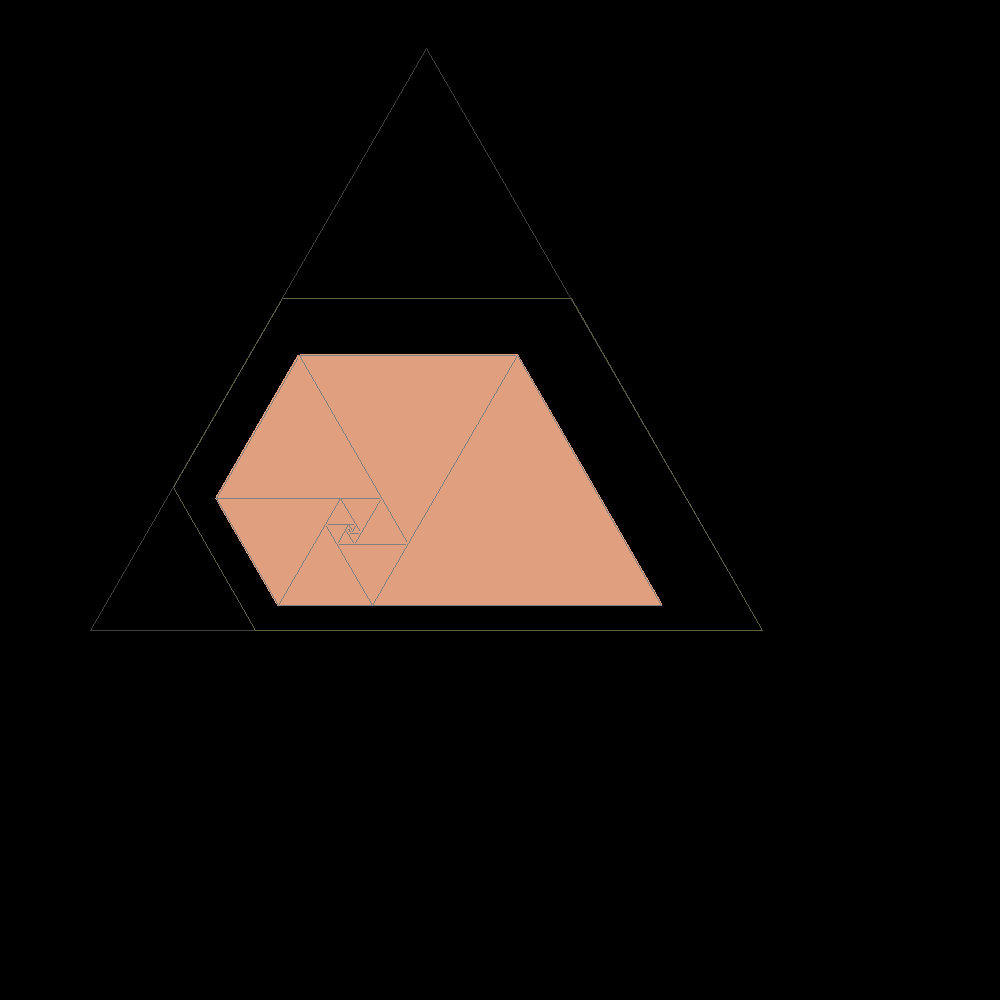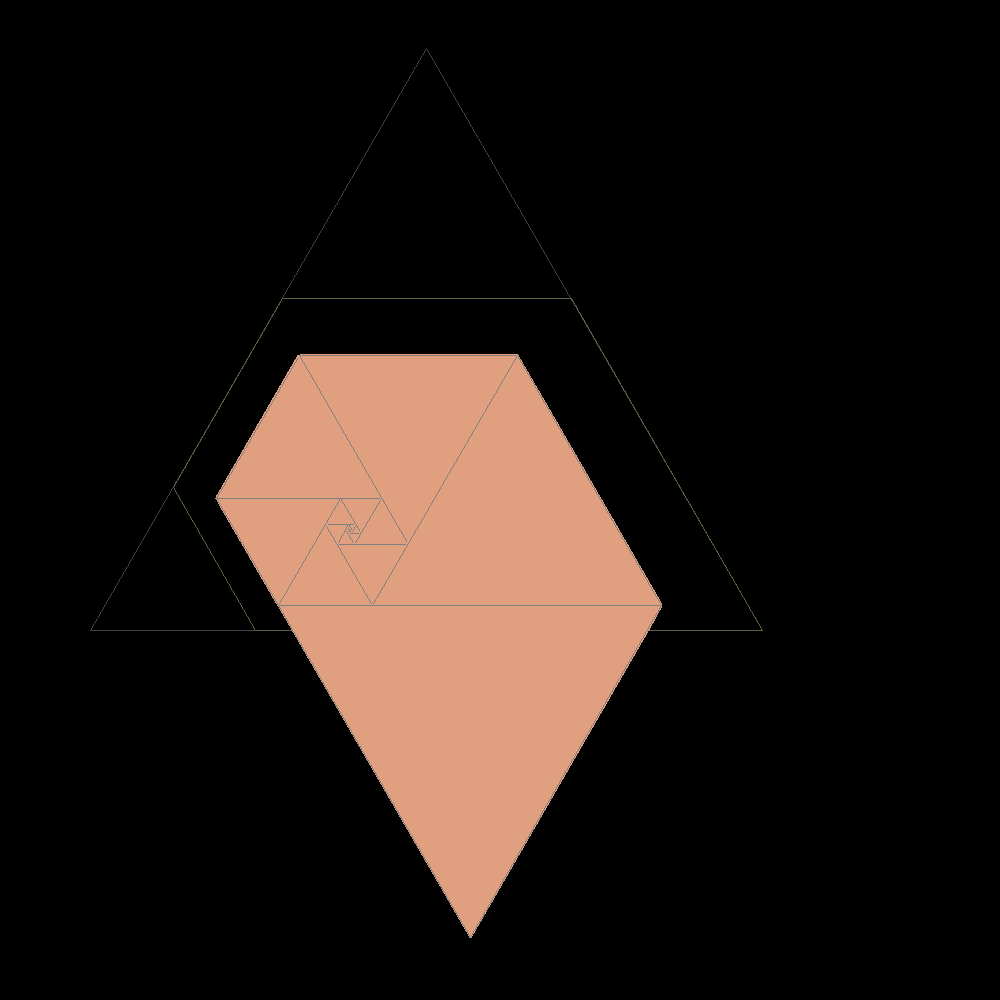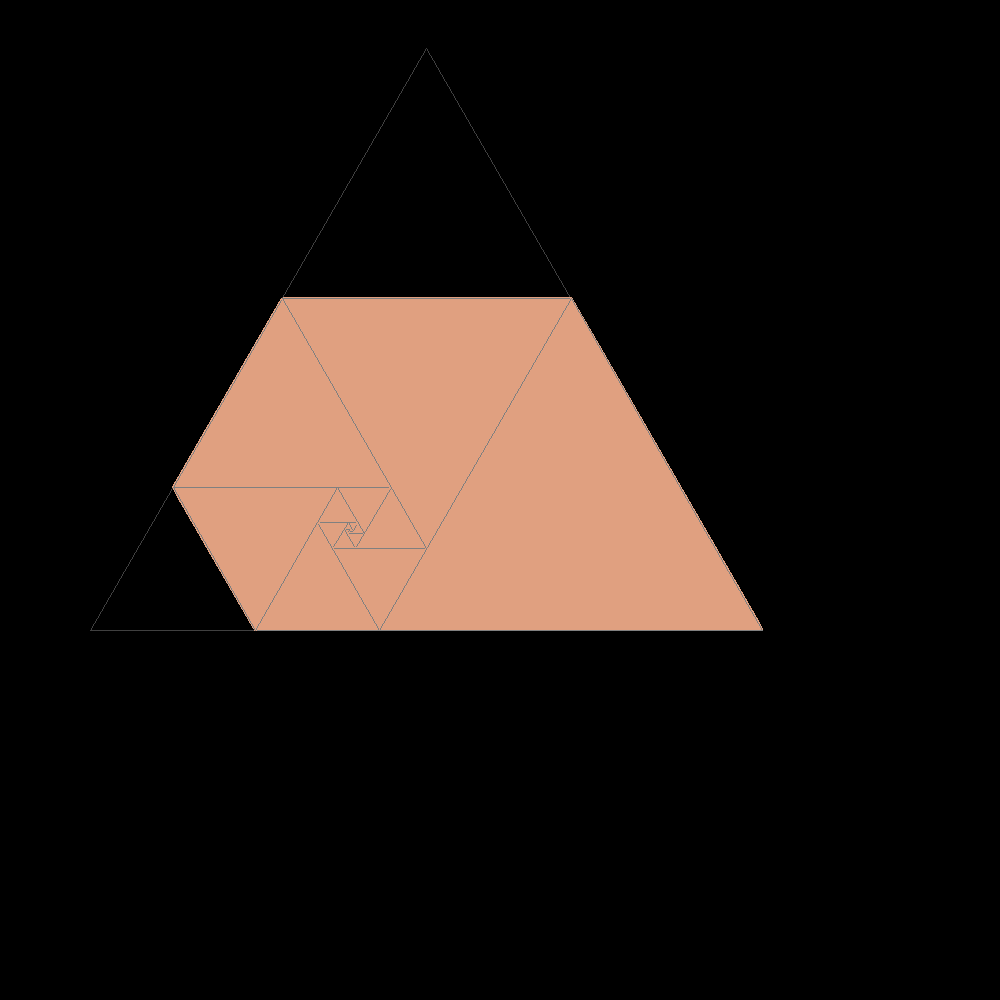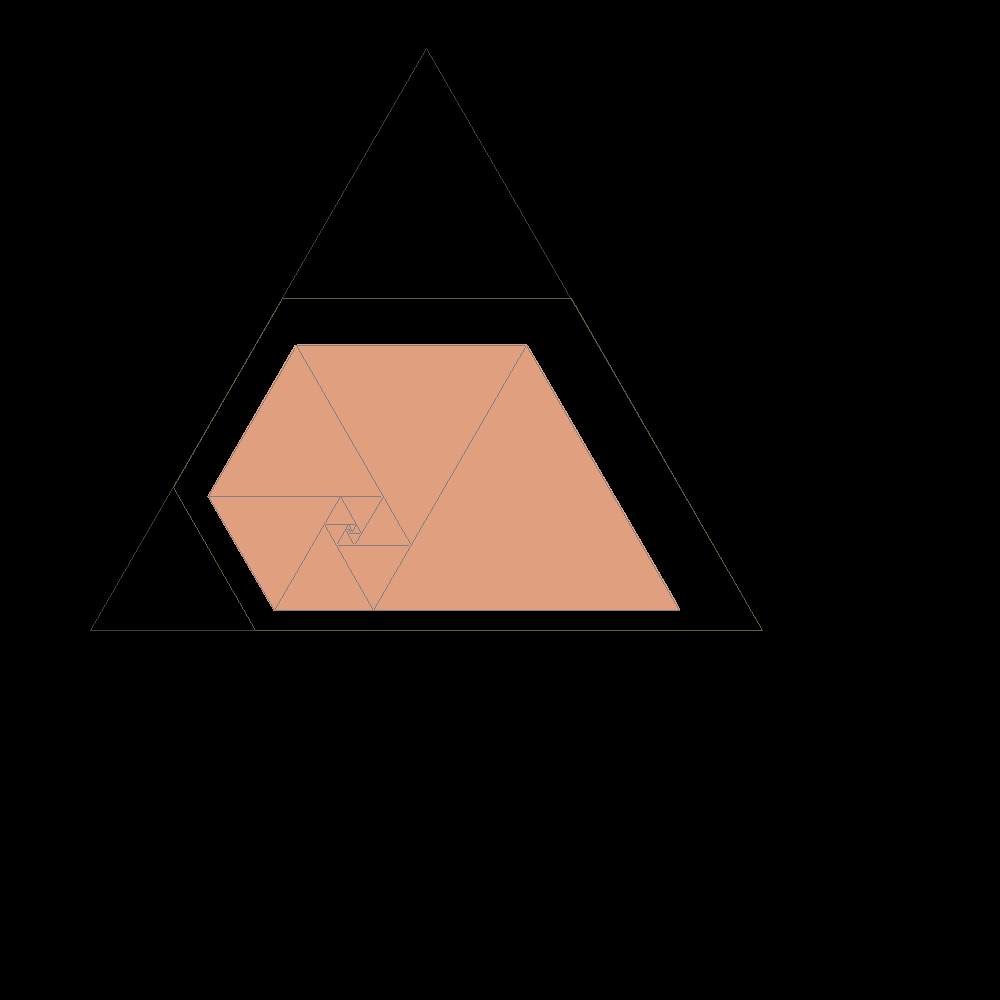Shortly after the result is confused with the plastic trapeze to which it tends

Plastic trapeze

packing and unpacking