|
| ||
|
Ultimo aggiornamento: 13/01/2013 |
||
|
| ||
|
Piergiorgio Odifreddi “UNA VIA
DI FUGA", IL GRANDE RACCONTO DELLA GEOMETRIA, OSCAR MONDADORI, 2012
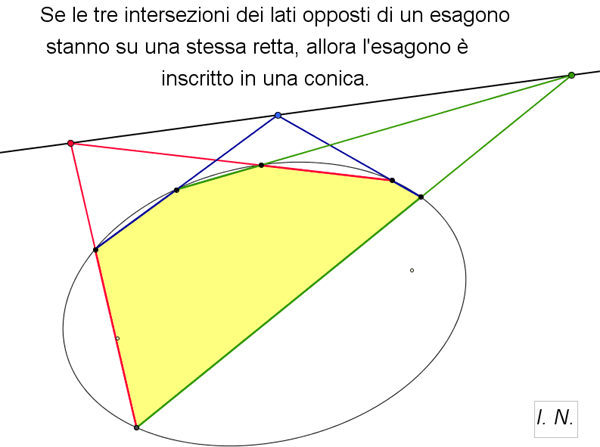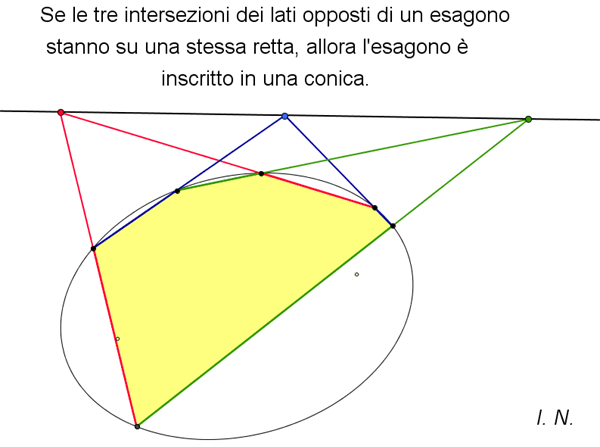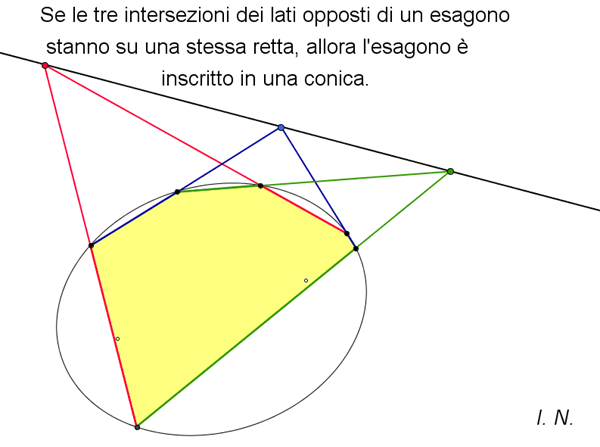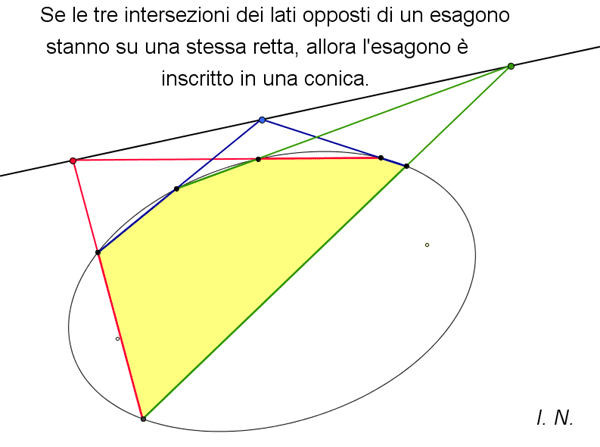
(Pagine 254) In questo secondo libro, che fa parte di una specifica trilogia, l'autore narra la storia del periodo moderno della geometria, periodo che si estende dall'entrata in scena degli Arabi fino a una conclusione (non definitiva!) situata verso la fine dell'Ottocento. Tale periodo è caratterizzato, come precisa l'autore stesso nella Premessa, da un ripensamento globale dei fondamenti euclidei. Partendo dalle grandi e astratte decorazioni policrome dell'Alhambra (gli Ebrei e gli Arabi si rivolsero all'arte astratta, accettando la costrizione radicale "Non ti farai idolo né immagine alcuna di quanto è lassù nel cielo, né di quanto è quaggiù sulla terra, né di ciò che è nelle acque sotto la terra" ) e analizzandole matematicamente, si passa alla rivoluzione della prospettiva e del punto di fuga nel Rinascimento, da Brunelleschi, a Desargues e ai teoremi di Pascal. Il terzo capitolo è dedicato a Eulero. Viene, poi, preso in considerazione il Giappone che tra il 1633 e il 1854 visse un paio di secoli di autarchia culturale e la matematica ebbe uno sviluppo autoctono, in seguito chiamato wasan (da Wa "Giappone" e san "matematica"). Reputo interessanti i sangaku "tavolette matematiche", la più nota e singolare espressione wasan. I sangaku erano una specie di ex voto offerti in omaggio a qualcuna delle innumerevoli divinità dello Shintoismo e del Buddhismo, venerate nei luoghi sacri in cui venivano appese le tavolette; queste costituivano, probabilmente, sfide intellettuali per i visitatori, oppure pubblicità per le scuole da cui provenivano. La ricerca di una dimostrazione per il postulato euclideo delle rette parallele accompagna la narrazione e l'autore ci guida in quella parte del mondo matematico dove gli audaci, grazie alla loro curiosità e tenacia nell'affrontare nuovi percorsi cercando altre verità, scardinarono gli schemi del passato e riuscirono a scoprire che quella degli Elementi è solamente una delle possibili geometrie. Grazie a matematici, quali, ad esempio, Saccheri, Bolyai, Lobačevskij, Gauss, Riemann e Beltrami, viene trovata la "via di fuga" dalla gabbia euclidea e si affermano altre verità che consentono opportune interpretazioni della geometria della Natura. Personalmente ritengo che sia stato realizzato prioritariamente un libro di matematica, dove i teoremi vengono illustrati e dimostrati in modo rigoroso, ma l'autore, ben consapevole che determinati passi, squisitamente tecnici, potrebbero stancare l'eventuale lettore non matematico, da abile professionista qual è, sa ricorrere, al momento giusto, a riferimenti più abbordabili e attraenti, come gli esempi presi dall'arte, dall'architettura, dalla letteratura e dalla vita quotidiana, non dimenticando di inserire, con il consueto stile disinvolto e brillante, anche battute ironiche, originali e simpatiche, che caratterizzano il suo modus scribendi e che possono rassicurare piacevolmente il lettore non "addetto ai lavori". A cavallo tra Ottocento e Novecento si era ormai compreso che la geometria euclidea non rappresentava più l'unico linguaggio in cui è scritto il grande libro della Natura. La geometria iperbolica aveva evidenziato un altro linguaggio, alternativo a quello euclideo, altrettanto valido a descrivere aspetti significativi del mondo esterno. In seguito, nel Novecento, furono scoperti altri linguaggi geometrici e alla descrizione della loro Babele sarà dedicato l'ultimo volume della trilogia.
Alcune animazioni che hanno tratto
spunto dalla lettura del libro "UNA VIA DI FUGA"
Arrotondamento: 1 cifra decimale
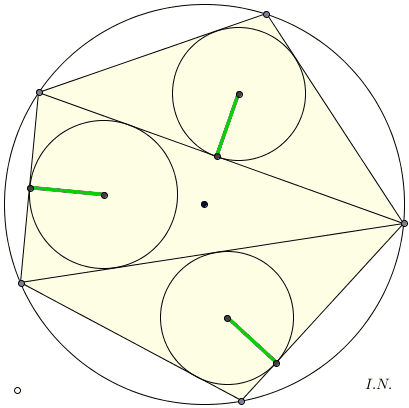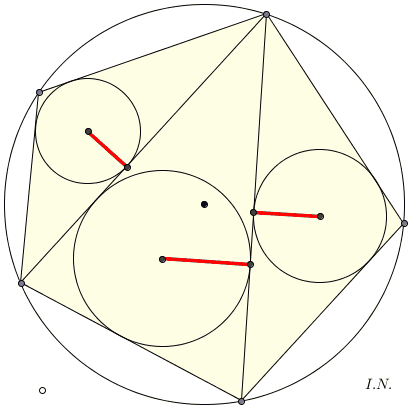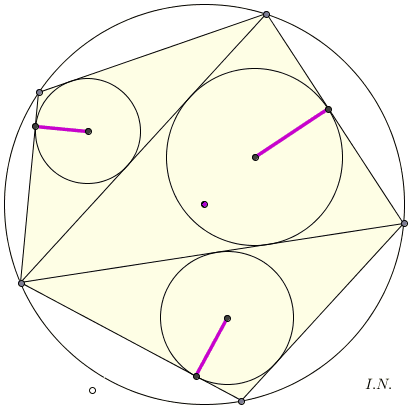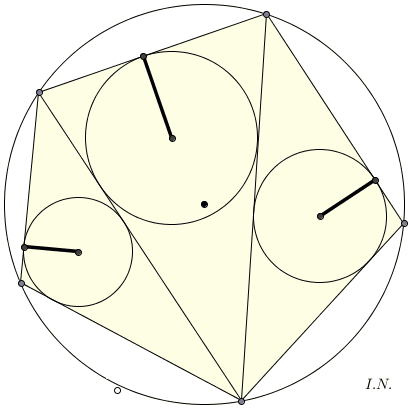
TEOREMA GIAPPONESE (dai sangaku)
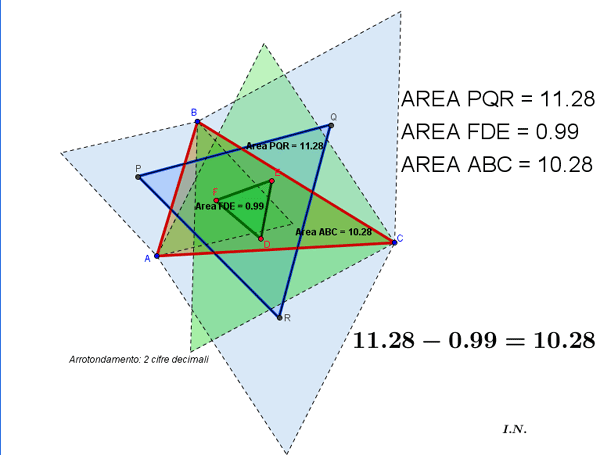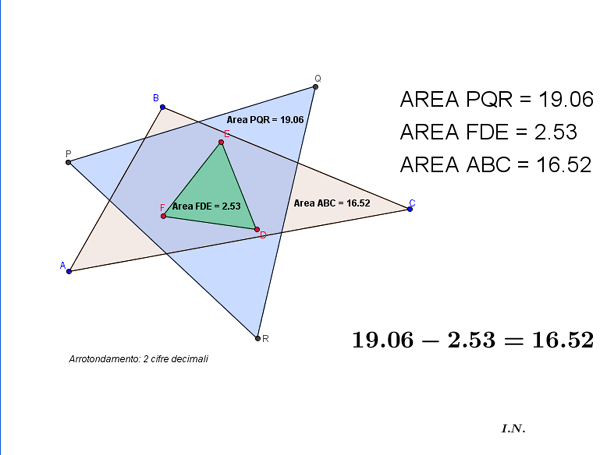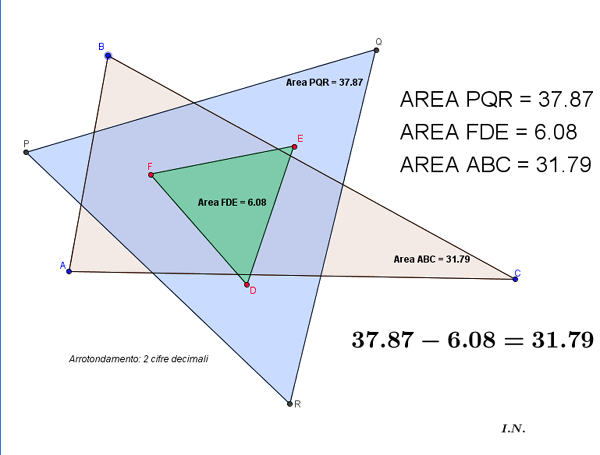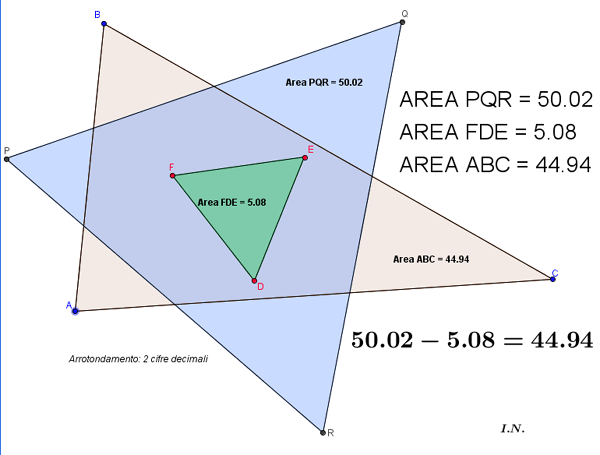
TEOREMA DI NAPOLEONE (almeno apparentemente
dovuto a Napoleone)
Infine, segnalo un gioco topologico, presente nel volume, da me proposto
agli/alle alunni/e del Primo Circolo di Sassari:
| ||