|
Piergiorgio Odifreddi “ABBASSO EUCLIDE!", IL GRANDE RACCONTO DELLA GEOMETRIA
CONTEMPORANEA, MONDADORI, I edizione marzo 2013
(Pagine 370)
Questo terzo libro, dedicato alla geometria contemporanea, rappresenta
la terza parte di una trilogia, concludendo il racconto
illustrato che ha avuto inizio in
C'è spazio per tutti ed è continuato in
Una via di fuga .
Nella
Premessa
"Morto il re, viva il re!" l'autore spiega come il congresso su "La
nuova matematica", avvenuto a Royaumont, nei pressi di Parigi, fu ricordato
soprattutto per la provocatoria conferenza "Abbasso Euclide!"
tenuta da Jean Dieudonné, membro originario del gruppo Bourbaki.
Si attaccava il passato per proporre, nell'insegnamento, sia la sostituzione
dell'aritmetica e della geometria con le strutture bourbakiste, sia
l'abbandono del linguaggio dei numeri e dei punti in favore della
terminologia insiemistica. Purtroppo, già nel 1960 venne istituita la
Commissione europea di Dubrovnik con l'incarico di riscrivere i programmi
delle scuole medie e superiori e ben presto mezzo mondo fu contagiato dal
morbo bourbakista. Ma allora perché è stato scelto il titolo "Abbasso
Euclide"? Semplicemente perché si tratta di un grido di incitamento ad
ampliare e ad arricchire i nostri orizzonti e, riformulato in maniera
positiva e costruttiva, ha entusiasticamente il significato
dell'esclamazione"viva" la geometria, senza alcuna "catena " limitativa
euclidea!
Il filo conduttore resta quello di illustrare la geometria attraverso
l'arte. La geometria e l'arte moderna, l'una in maniera più razionale e
l'altra in modo più artistico, si concentrano sulle forme pure. La geometria
aiuta a capire e a spiegare l'arte contemporanea e quest'ultima illustra la
geometria.
Col suo stile
piacevole e denso di informazioni dotte, Piergiorgio Odifreddi ci guida,
attraverso un percorso avventuroso e
intellettualmente accattivante, alla scoperta delle varie geometrie che si
ritrovano in Natura e nell’arte.
Vengono prese in considerazione le geometrie multidimensionali, topologiche
e finite, senza che vengano trascurati i frattali e non manca
un'interessante riflessione sui fondamenti.
Proprio grazie alla teoria dei frattali la matematica moderna è riuscita a
mettere parzialmente ordine nel caos e nel caso.
Oggi si parla di "effetto Droste" perché a partire dal 1904 l'omonima
produttrice olandese di cacao adottò sulle sue scatole l'immagine di
un'infermiera che teneva su un vassoio una copia della scatola stessa.
Attualmente le strutture autosimili si possono realizzare e visualizzare con
facilità al computer tramite i processi iterativi tipici dei frattali.
EFFETTO DROSTE (animazione realizzata, nel 2004, da Giorgio Pietrocola)
http://www.maecla.it/bibliotecaMatematica/go_file/drostemm.htm
Alcune animazioni che hanno tratto
spunto dalla lettura del libro "ABBASSO EUCLIDE!"
Nel libro "ABBASSO
EUCLIDE!" di Piergiorgio Odifreddi viene descritto l'impaccamento di Leibniz
riportando quanto scritto da Leibniz stesso
in una lettera dell'11 marzo 1706 all'amico gesuita Bartolomeo Des Bosses:
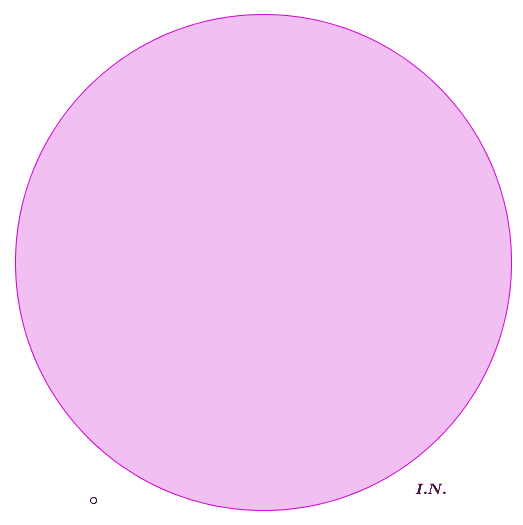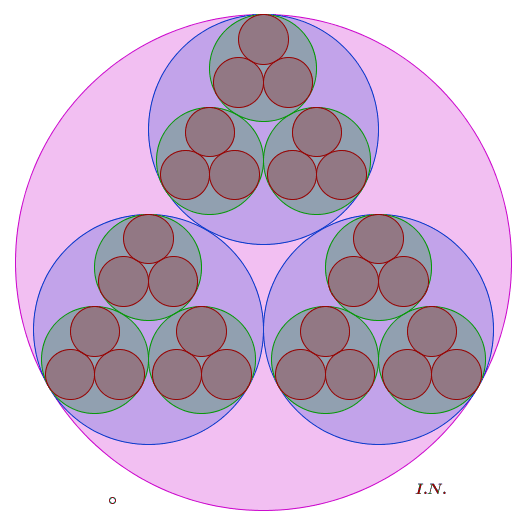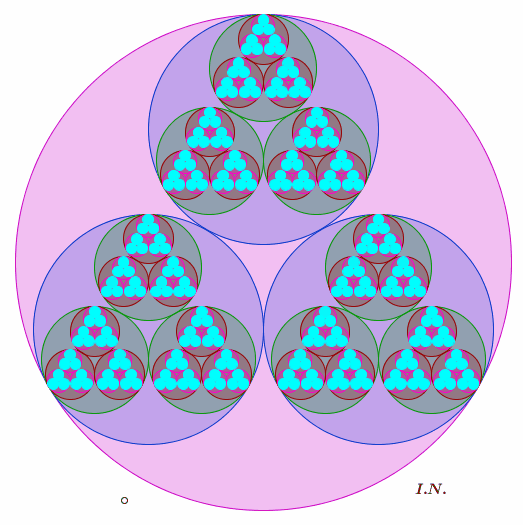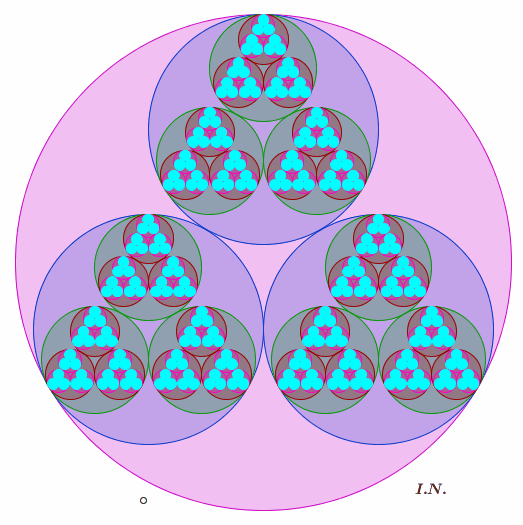
"Immagina un cerchio. Disegna in esso tre cerchi uguali, i più grandi
possibili.
Dentro ciascuno di essi disegna di nuovo tre cerchi uguali, i più grandi
possibili. E immagina di procedere in questo modo all'infinito..."
A me ricorda il triangolo di Sierpinski:
http://www.maecla.it/bibliotecaMatematica/pz_file/SIERPINSKI.ppt
Animazione di Giorgio Pietrocola (che ringrazio moltissimo!) inerente
all'impaccamento di Leibniz generalizzato

Filtro di Apollonio
È possibile realizzare varie forme del filtro di Apollonio: si parte da un
cerchio,
inscrivendogli due (o tre, o quattro ecc.) cerchi tangenti fra loro e a esso
e continuando a inscrivere cerchi tangenti in modo ricorsivo.
Continuo a ringraziare molto volentieri il matematico Giorgio Pietrocola
che ha realizzato la seguente
interessante animazione, inerente a varie forme del filtro di Apollonio

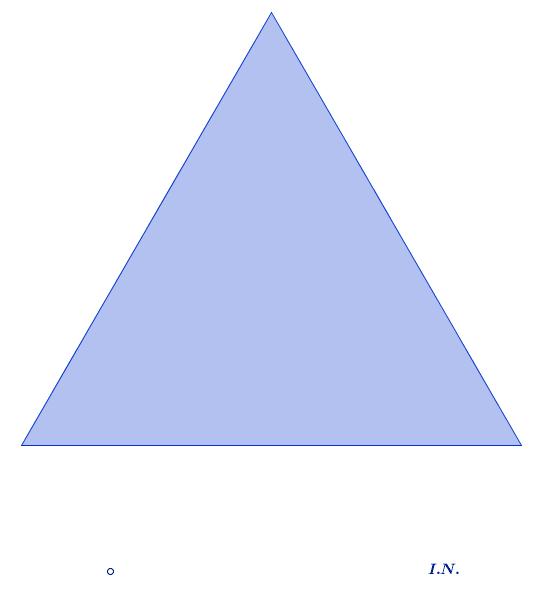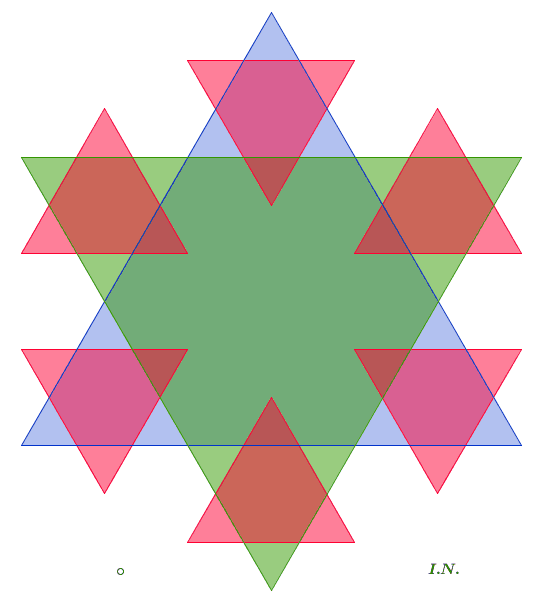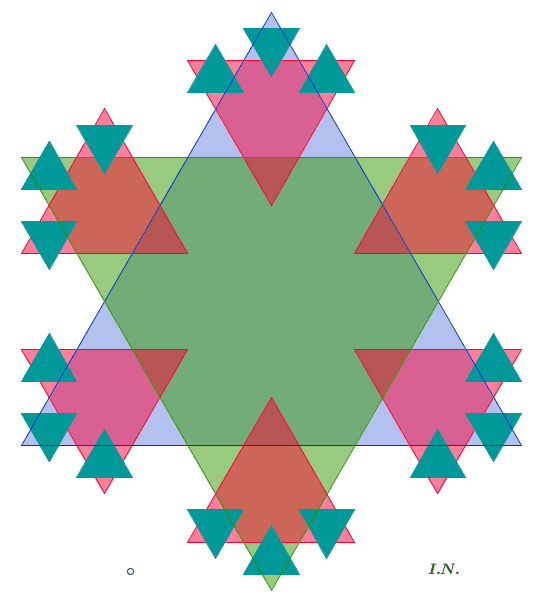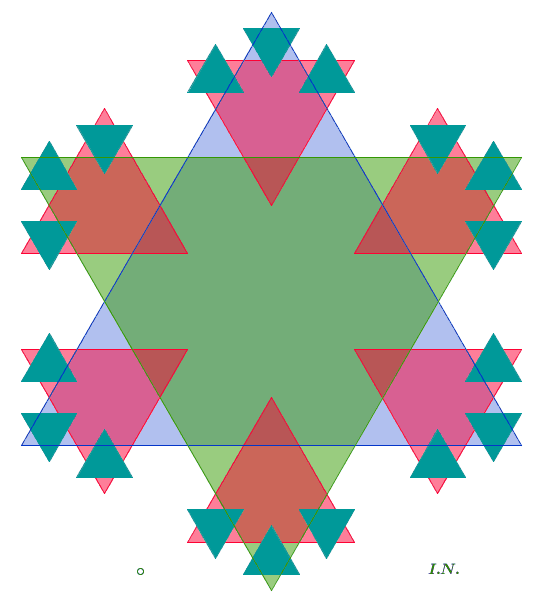
La CURVA DI KOCH può essere vista come il bordo della figura che si ottiene
partendo da un triangolo
equilatero e aggiungendone uno simmetrico che formi con esso una stella di
David e ripetendo il
processo sui triangolini esterni, all'infinito.
Il filtro di Sierpinski può essere anche definito per addizioni successive
di meandri della cosiddetta
CURVA A PUNTA DI FRECCIA.
Il procedimento consiste nel partire da un segmento, considerarlo come la
base di un triangolo equilatero,
e sostituirlo con una spezzata corrispondente al percorso che sale per metà
di un lato,
attraversa orizzontalmente il triangolo e scende per metà dell'altro lato.

|





