Ultimo aggiornamento: 26/05/2007

Joseph Novak "L'APPRENDIMENTO SIGNIFICATIVO - Le mappe concettuali per creare e usare la conoscenza", Erickson
Ringrazio Giovanna Maria Melis, che, nell'ottica della ricerca-azione affinché gli alunni possano usufruire di un apprendimento significativo,  ha segnalato tale libro, riportando quanto segue:<< Le tecniche di apprendimento tradizionali (purtroppo ancora molto diffuse) si basano spesso su un apprendimento meccanico, ovvero sulla trasmissione e l'acquisizione di conoscenze attraverso una pura e semplice memorizzazione di nozioni. 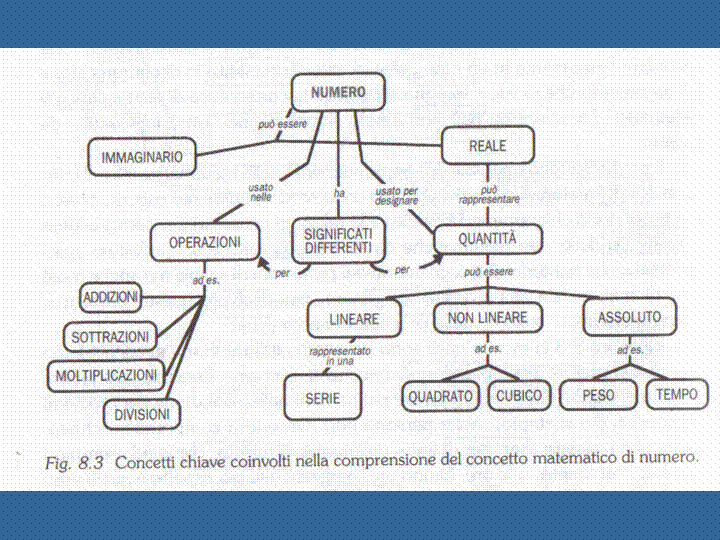Questo libro si pone l'obiettivo di favorire un tipo di apprendimento significativo, attivo e creativo, che permetta alle persone di scoprire, selezionare, collegare, mettere in relazione e generalizzare le nuove conoscenze attraverso l'utilizzo di uno strumento didattico/di studio efficace come le mappe concettuali.

A pagina 199, "Materiali per l'apprendimento", si legge: "I materiali utilizzati possono influenzare in modo positivo o negativo l'apprendimento. Ad esempio, degli studenti che hanno avuto esperienze negative con la matematica, davanti ad un compito educativo in cui sia coinvolta la matematica possono reagire negativamente, anche quando si trovano in un contesto fisico e culturale piacevole e possiedono conoscenze sufficienti sull'argomento. Che cosa dovrà fare l'insegnante in un caso come questo, in cui il livello di comprensione dell'argomento che so vuole insegnare richiede la conoscenza di alcuni concetti matematici? La soluzione può non essere semplice, ma non è impossibile da trovare. 

Il problema fondamentale dell'apprendimento della matematica sta nel fatto che molti dei materiali educativi utilizzati sono "concettualmente oscuri", ovvero non espongono chiaramente i concetti e le relazioni necessari per comprendere il significato delle idee matematiche da studiare. Questo è un problema quasi universale, che riguarda gli insegnamenti dei primi anni di scuola, ma anche molti corsi di matematica all'università. In genere, per risolvere questo problema, vengono insegnate soltanto delle procedure meccaniche. La figura 8.3 ci mostra quali sono i concetti più importanti di cui abbiamo bisogno per riuscire a comprendere il concetto di "numero".

Essa presenta inoltre l'origine di alcune delle fonti di errore più comuni nella risoluzione dei problemi matematici. Ad esempio, molte persone non riescono a comprendere chiaramente che i numeri usati per definire delle unità di misura, come ad esempio i grammi, i centimetri e le ore, hanno un significato diverso rispetto a quelli usati per compiere delle operazioni come l'addizione, la sottrazione, la moltiplicazione e la divisione. Mentre 2 + 2 può risultare 4 in un'operazione, 2 ore più 2 minuti corrisponde a 122 minuti e non a 4 ore o a 4 minuti.

Il professor Henderson, collega e illustre matematico, nell'aiutarmi a costruire la figura 8.3, mi confidò di essere riuscito ad accorgersi molto tardi nella sua carriera dell'acuta distinzione che io avevo compiuto. Non è così ovvio che esistano due significati distinti di "numero", uno per rappresentare delle unità di misura e l'altro usato in operazioni come addizione o divisione. L'incapacità di comprendere in modo chiaro i concetti elementari della figura 8.3 è una delle ragioni per cui la matematica genera così tanta confusione in molte persone. I problemi inoltre si moltiplicano quanto più aumenta la complessità dei concetti matematici o quando si considerano le applicazioni della matematica alle scienze o ad altri campi. Il risultato a lungo termine può essere definito "ansia da matematica", sperimentata da così tante persone; molte ricerche sulle cause di questo tipo di ansia non prendono nemmeno in considerazione però l'oscurità concettuale di quasi tutti gli insegnamenti di matematica o delle materie che implicano l'uso di concetti matematici. Credo che se ci si sforzasse di rendere la matematica concettualmente trasparente, essa potrebbe diventare uno degli argomenti più facili e gratificanti da studiare. So benissimo che solo una piccolissima parte della comunità matematica è d'accordo con me su questo, anche se negli anni il consenso sta progressivamente aumentando" >>

(Cliccate sopra l'immagine della mappa concettuale di Novak, per vederla ingrandita)

Ritengo interessante trascrivere un commento del collega Giorgio Pietrocola (che ringrazio) riguardo alla mappa concettuale di Novak: << I numeri immaginari sono solo un sottoinsieme dei numeri complessi che, a loro volta, sono un ampliamento dei reali e non certo un insieme disgiunto, come sembra indicare la mappa. La cosa peggiore, comunque, mi sembra la confusione tra numero e funzione. Non sono i numeri, che io sappia, a essere lineari o non lineari, ma le funzioni.Confondere il concetto di numero con quello di funzione è utile? Non vedo proprio come uno schema del genere possa aiutare qualcuno a capire qualcosa di significativo. Novak scrive: "Credo che se ci si sforzasse di rendere la matematica concettualmente trasparente, essa potrebbe diventare uno degli argomenti più facili e gratificanti da studiare" Questo mi sembra un grave errore. I concetti elementari della matematica sono tutt'altro che trasparenti, come riassunse Bertrand Russell  con la sua famosa boutade, dicendo: "La matematica è una scienza in cui non si sa di che cosa si parla, né se ciò che si dice è vero." Oggi sappiamo che non tutto può essere definito in modo chiaro e trasparente. Concetti fondamentali, come quelli di numero e di punto, si considerano concetti primitivi che non possono essere definiti se non, con un certo margine, dalle relazioni che li coinvolgono." Ciò che serve per capire in modo significativo, a mio avviso, non sono definizioni chiare, ma una esperienza operativa concreta e autonoma, da far evolvere progressivamente e sintonicamente in un pensiero formale. Del resto, se noi dovessimo parlare quotidianamente ed esprimerci solo con parole di cui conosciamo l'esatta definizione, probabilmente dovremmo tacere. Elliot Mendelson, nel suo classico "Introduzione alla logica matematica", Ed. Boringhieri, nell'introduzione al suo trattato, scrive: "Definizioni rigorose hanno poco valore all'inizio dello studio di una certa disciplina; il modo migliore per scoprire di che cosa tratti la logica matematica consiste nell'iniziare a praticarla...

Mi piacerebbe ascoltare la testimonianza di qualcuno a cui una mappa del genere è risultata effettivamente utile. Naturalmente intendo utile non per propinarla ad altri, ma per il proprio, effettivo e significativo apprendimento.>>

Riporto quanto scritto da Giovanna Maria Melis, che ringrazio ancora per la segnalazione del testo e, in particolare, della mappa concettuale inerente al "numero", testo e mappa che hanno stimolato una costruttiva discussione tra noi insegnanti; dopo il commento di Giorgio Pietrocola, ecco la "riflessione" di Giovanna Maria Melis: "Mi sto muovendo nell'ambiente del corso "ForTic", che mi permette non solo di "praticare" la
mia naturale curiosità e di ampliare le mie conoscenze, ma anche -come in questo caso - di ridefinirle e di correggerle.
Questo approfondimento poi, mi invita a una maggiore cautela: anche testi di qualità (a me il libro di Novak è piaciuto e lo ritengo utile e valido dal punto di vista educativo) contengono errori, che possono generare errate convinzioni."
Credo che quanto scritto da Giovanna sia pienamente condivisibile; nell'ottica di un apprendimento continuo nell'arco dell'intera vita, riteniamo che il confronto tra docenti di ogni ordine e grado sia arricchente, non solo per favorire la continuità educativa e didattica, ma anche per una decostruzione e ricostruzione collaborativa dei saperi, seguendo il paradigma pedagogico del costruttivismo sociale.