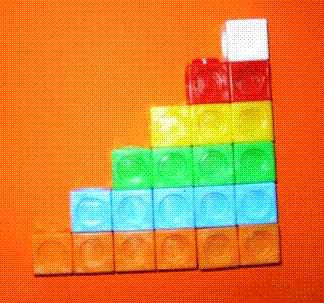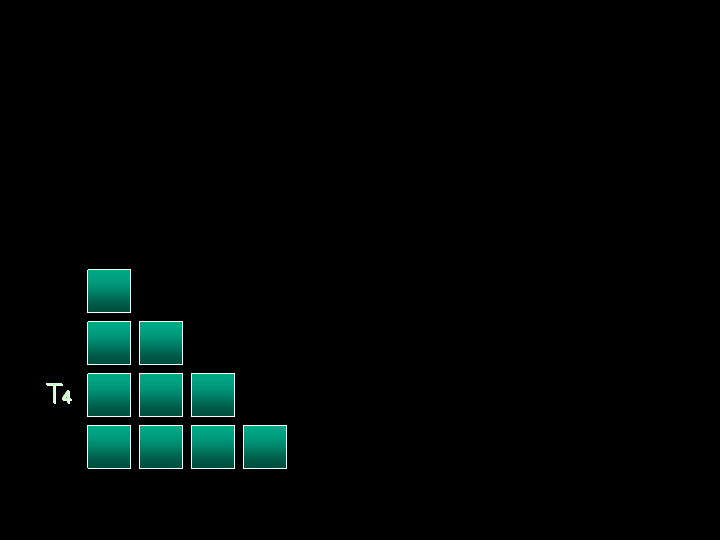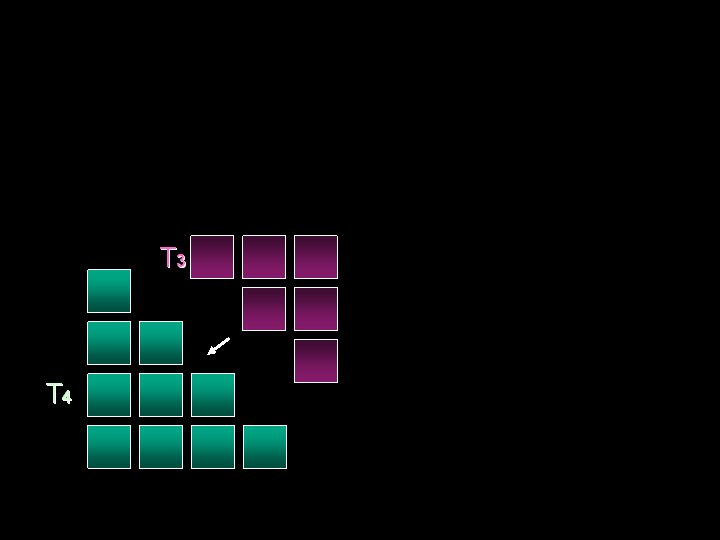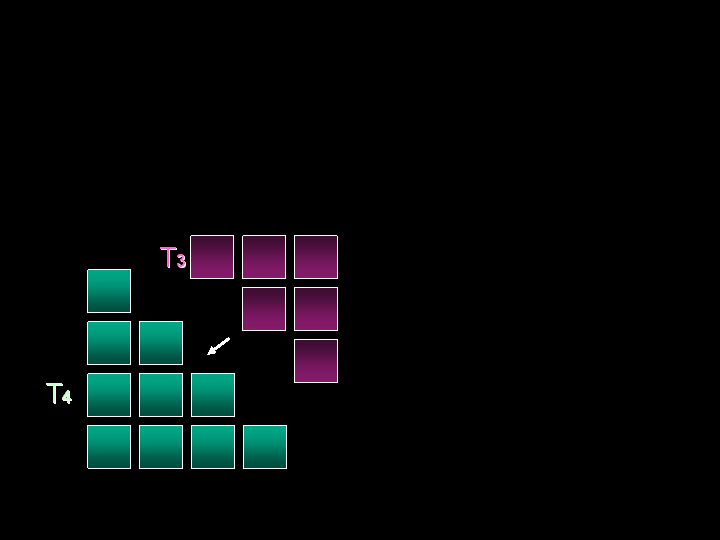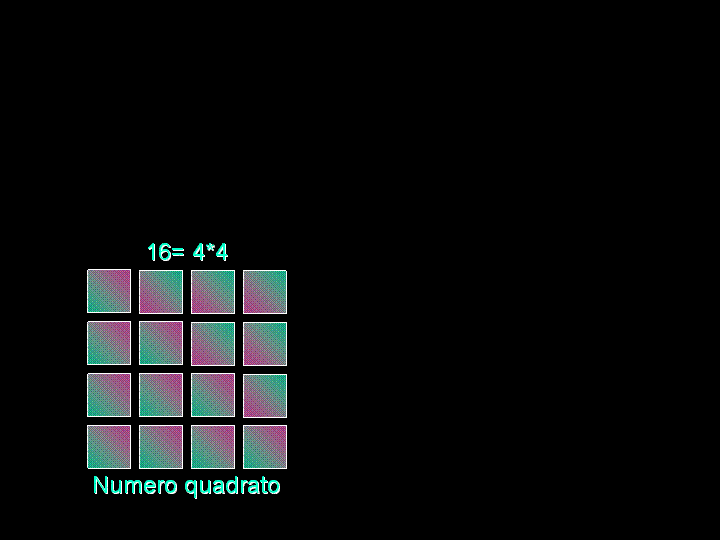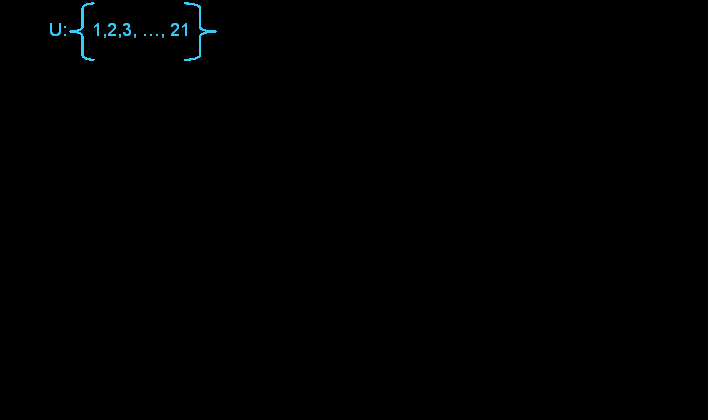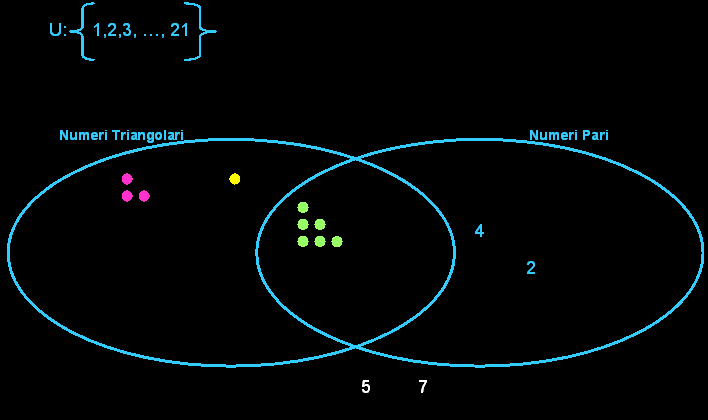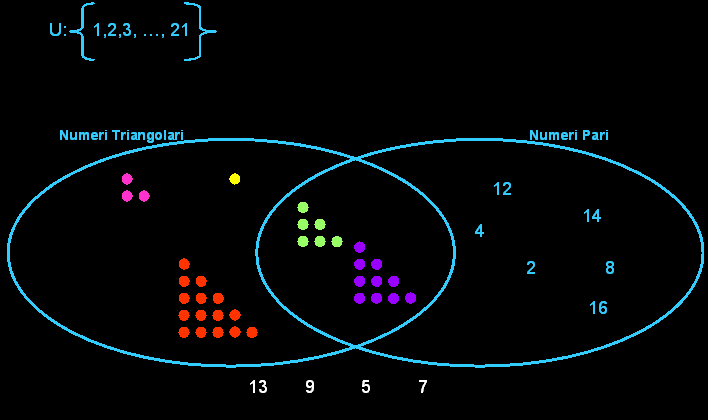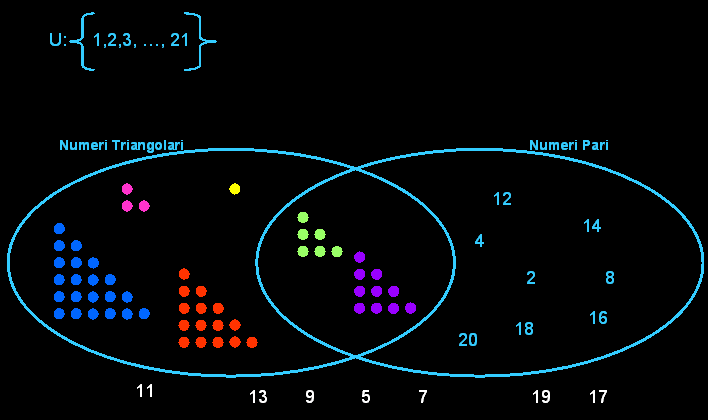NUMERI TRIANGOLARI

Davvero la matematica offre la possibilità di sviluppare immaginazione numerica e geometrica nei bambini, e non solo. Andare a curiosare in questa rete di relazioni per scoprire come si combinano i numeri tra loro e re-inventare regole che permettono di trovare altri numeri è un processo di ricerca stimolante e vivacemente attivo.
Questa attività segue il lavoro sui numeri quadrati – affrontati anche in classe quarta – e illustra il percorso dei bambini che, partendo da una base esperenziale concreta, sono arrivati a sviluppare alcune conoscenze intuitive matematiche.

In classe terza, dopo aver osservato i numeri quadrati, i bambini hanno notato che disponendo il materiale in modo diverso si poteva ottenere un’altra figura: il triangolo.


 

Per scoprire da dove si ‘ricavano’ i numeri triangolari, e ricordando le attività precedenti, i bambini hanno proposto di disegnare i numeri in righe di lunghezza crescente e di scrivere i numeri con l’albero.
Si sono accorti che le cifre da usare erano diverse da quelle scritte nell’albero dei numeri dispari, che aveva fatto trovare i numeri quadrati. 
Infatti, dopo l’uno, si doveva scrivere 1+2, perché la seconda riga conteneva due quadretti. In questo nuovo albero sono presenti in successione ordinata sia i numeri dispari che i pari.

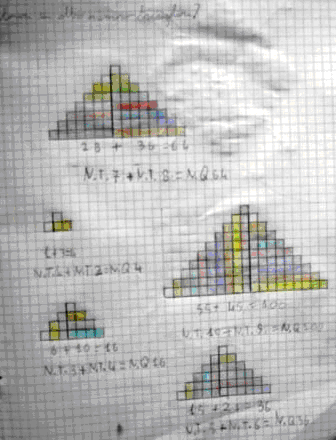
                                                    1

                                                    1+2=3

                                                    1+2+3=6

                                                    1+2+3+4=10

                                                    1+2+3+4+5=15

                                                    1+2+3+4+5+6=21

                                                    1+2+3+4+5+6+7=28

                                                    1+2+3+4+5+6+7+8=36

                                                    1+2+3+4+5+6+7+8+9=45

                                                    1+2+3+4+5+6+7+8+9+10=55
sommando i numeri delle righe troviamo i numeri triangolari.
Con la carta strutturata a puntini i bambini hanno costruito i primi numeri triangolari:

Queste le regole per i numeri triangolari che sono state scoperte da tutti bambini

così è più semplice trovare il numero triangolare successivo:
55+10=65
65+1=66
66+11= 77
77+1= 78
Una sequenza animata illustra questa regola:

Carla ha anche osservato che nella sequenza ordinata dei numeri triangolari è presente un ritmo:
DispariDispari – PariPari – DD – PP -  ….
1   3    6    10   15    21    28    36, …
osservando i numeri triangolari in successione, si incontrano due numeri dispari seguiti da due numeri pari

ALTRE SCOPERTE

 Giocando con i modellini di carta che ogni bambino ha costruito, si sono fatte altre scoperte:

Due numeri triangolari consecutivi danno un numero quadrato:

T1+T2= Q2
1  + 3= 4

Osservazioni dei bambini
Si compongono numeri triangolari per trovare dei numeri quadrati

Combinando i modellini dei numeri triangolari, i bambini hanno trovato anche dei numeri rettangolari:

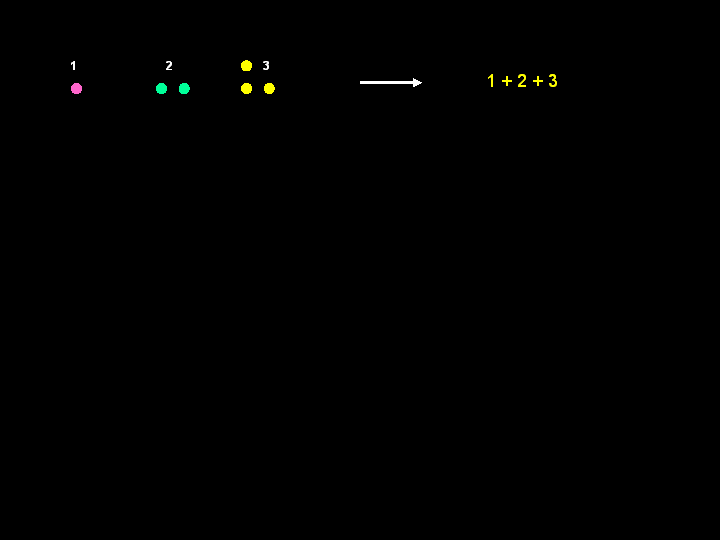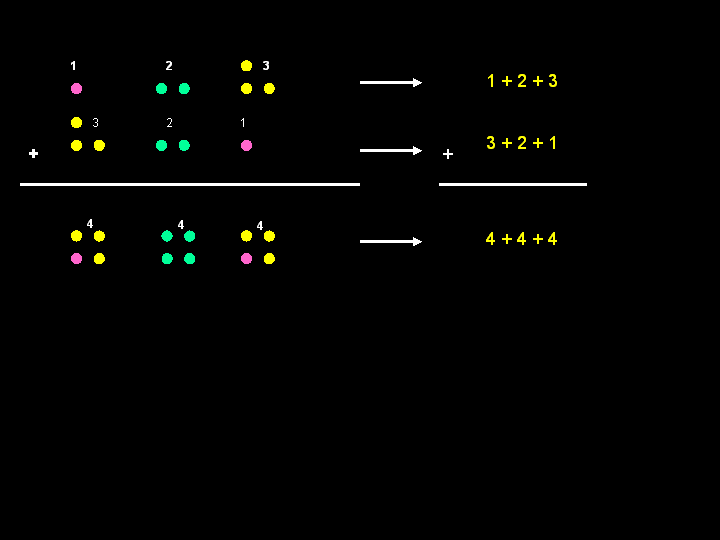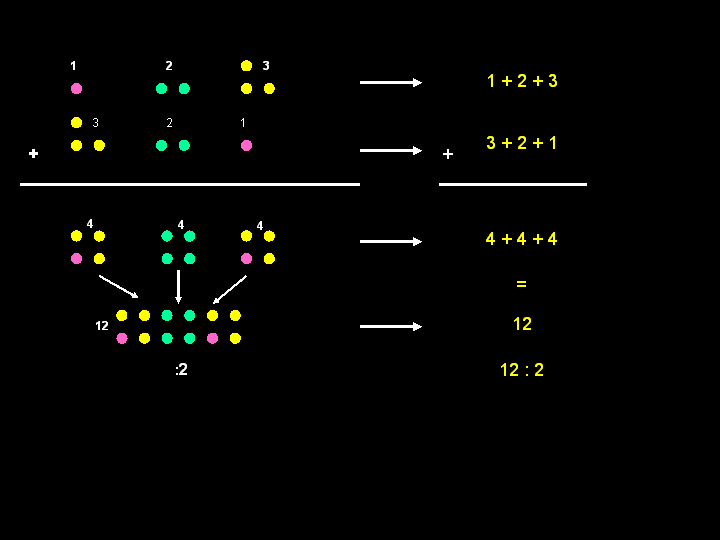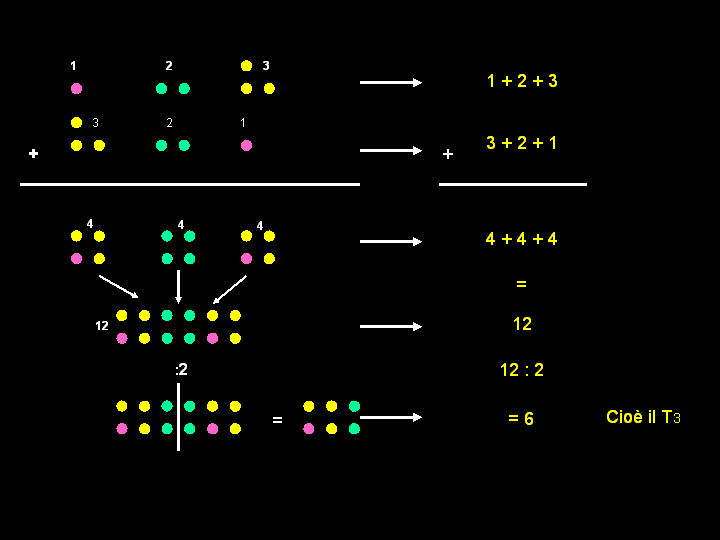
 UNA STRATEGIA PER TROVARE DEI NUMERI TRIANGOLARI

Se volessimo trovare il settimo numero triangolare, senza però dover fare il disegno, c’è questo ‘trucchetto’ che utilizza proprio la regola già scoperta sui numeri triangolari.
Abbiamo detto il settimo numero triangolare?
Scriviamo allora la sequenza dei numeri naturali fino al 7:
1ª somma: 1+2+3+4+5+6+7
e gli stessi numeri, solo scrivendoli all’inverso:
2ª somma : 7+6+5+4+3+2+1
ora sommiamo ciascun addendo della prima somma con ciascun addendo della seconda somma,
e otteniamo:
8+8+8+8+8+8+8

 

1+2+3+4+5+6+7
e gli stessi numeri, solo scrivendoli all’inverso:
7+6+5+4+3+2+1

 

sommiamo ciascun addendo della prima somma  con ciascun addendo della seconda somma, e otteniamo:
8+8+8+8+8+8+8
l’8 è ripetuto sette volte, perciò:
8x7=56
Dividiamo 56 per 2 e si ottiene 28, che è il settimo numero triangolare
 

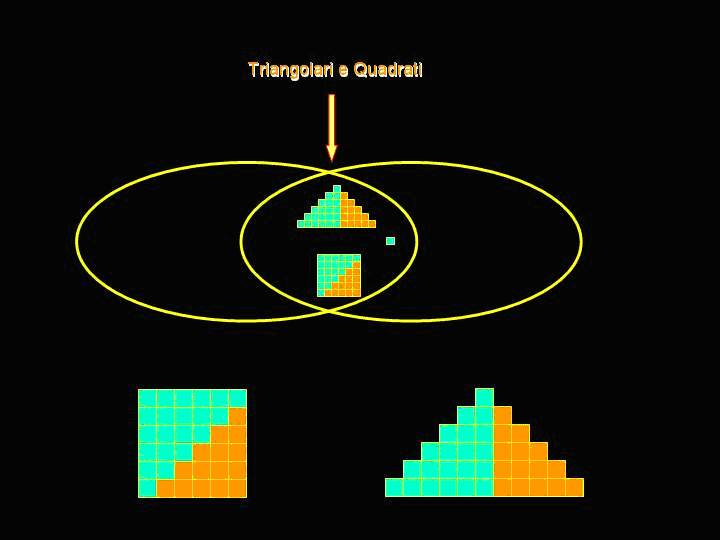
QUALCHE CLASSIFICAZIONE

Il diagramma di Eulero- Venn ci ha permesso di classificare i numeri triangolari secondo più attributi.
In questa classificazione abbiamo trovato numeri che sono triangolari e quadrati. In questo caso, 1 e 36

Questa animazione illustra la classificazione secondo gli attributi: essere triangolari e pari, partendo dal numero 1 fino ad arrivare al numero 21.

Nell’intersezione trovano posto i numeri 6 e 10, che sono triangolari e pari.
Nella regione a sinistra ci sono solo i numeri triangolari, in questo caso , 1- 3- 15 - 21
Nella regione a destra ci sono solo i numeri pari; in questo caso: 2 – 4 – 8 – 12 – 14  – 16 – 18 – 20.
Nella regione esterna, i numeri non triangolari e non pari, in questo caso: 5 – 7 – 9 – 11 – 13 – 17 – 19

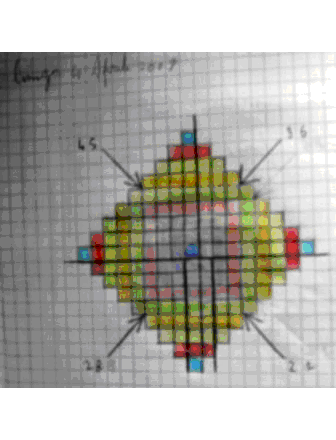
DIAGRAMMA AD ALBERO
Con un’altra classificazione possiamo trovare alcuni numeri triangolari e palindromi

 

In questo caso, l’animazione descrive il diagramma ad albero con tre attributi:

a-     essere pari

b-     essere numero triangolare

c-      essere numero palindromo

e in questa serie di numeri, U:   1,2,3,…,66
quelli che possiedono tutte le caratteristiche sono: 6 e 66

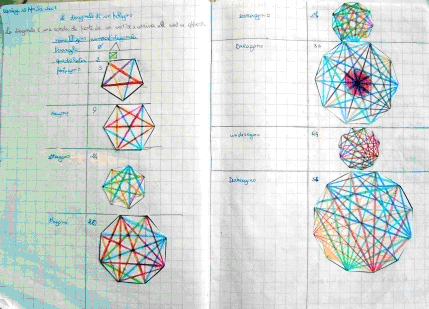
LEGAME TRA I NUMERI TRIANGOLARI E NUMERO DI DIAGONALI DEI POLIGONI

Una scoperta davvero insolita, che non mi aspettavo e che non conoscevo, ha avuto un seguito dopo un’attività di geometria. In classe si lavorava con corde per individuare le diagonali nei poligoni.

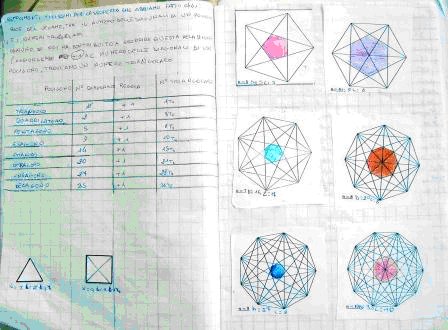
Dopo aver provato concretamente,  siamo passati a rappresentare con il disegno . Ho preparato delle schede di lavoro, utilizzando la carta a puntini . Alcuni bambini, poi, si sono lamentati del fatto che non riuscivano a tracciare con i pastelli  tutte le diagonali nei poligoni con un alto numero di lati. Ho allora consegnato ad ogni bambino dei modelli in cui erano già state tracciate le diagonali. Si trattava di ripassarle con i pastelli.

Successivamente, tutti insieme, abbiamo costruito una tabella di riepilogo:

Ed è proprio osservando il numero delle diagonali che abbiamo trovato un ‘legame’ tra queste e i numeri triangolariJ

Con un’altra tabella si chiarisce meglio questa relazione:

Abbiamo provato a definire questa scoperta, ovviamente per quanto riguarda i poligoni da noi considerati, e cioè dal triangolo al decagono:
“Aggiungendo +1 al numero delle diagonali di un poligono, troviamo un numero triangolare”o, al contrario: “ Togliendo 1 ad un numero triangolare, troviamo il numero delle diagonali di un poligono”.

Classe terza di Caniga, insieme con l'insegnante Maria Giovanna Melis