|
In uno scambio di mail nel gruppo sulla
COmunicazione ho narrato di un famoso matematico che avrebbe
affermato: '' Più studio la Matematica e meno la capisco!''. Ivana
Niccolai mi ha fatto notare con il solito garbo che lei non era a
conoscenza di un detto simile. Allora (siccome non è donna da prendere
alla leggera) mi sono dato da fare per trovare sul web notizie relative
a questa massima, ma, ahimè, senza risultato. Sforzando dunque la
memoria ho frugato nei recessi della mia mente e mi sono ricordato in
quale occasione l'ho sentita per la prima volta. Fu dalla bocca del mio
relatore, il quale la attribuiva ad un chiarissimo professore benemerito
dell'Università degli Studi di Bari.
In realtà l'ho subito fatta mia, perché ho creduto di afferrare al volo
il significato di questa massima.
Già, ma che significa "capire"? Perché, in fondo, anch'io ho ritenuto di
aver capito questa massima?
Lo sforzo che compierò in quest'articolo sarà quello di illustrare ciò
che ''ho capito del capire''.
Chi ha capito che cos’è un cavallo? Come riconosciamo un cavallo,
insomma? La risposta che mi sento di dare è che ne abbiamo visto da
bambini un bel po’ e dunque ce ne siamo fatti una rappresentazione
mentale con una descrizione schematica del tipo: un animale alto,
quadrupede munito di zoccoli, con gambe lunghe e sottili, con una testa
oblunga, occhi a palla sui due lati della testa, pelo corto sul corpo,
ma molto lungo sulla nuca, detto criniera, una coda molto lunga di peli
sottili e fluenti e così via... Dopo un po’ siamo in grado di
riconoscere tutti i cavalli del mondo.
Se questo va bene per le cose del mondo reale, che cosa dire per gli enti
astratti della Matematica? Prima di tutto vorrei precisare che la
Matematica, a differenza di quanto hanno provato a propagandare il bourbakismo ed Hilbert, è sì pensiero che si è astratto dal contesto, ma
non può fare a meno del contesto. In altre parole le cose nuove
diventano chiare quando sono immerse in ambienti la cui frequentazione è
ben consolidata dalla pratica. Basti pensare al numero naturale, poi
razionale assoluto, poi relativo, infine reale e complesso, fino ad
arrivare ai quaternioni. Oppure ricordiamo anche i modelli di geometria
ellittica o iperbolica costruiti con figure della geometria euclidea. Il
metodo assiomatico, proprio a partire da Euclide, tanto successo ha
riscosso perché gli assiomi traducono proprietà grafico- visive delle
figure: retta, piano, circonferenza etc. Basti pensare all’elegante
aggiramento del concetto di infinito di quello che adesso viene, in
molti manuali della scuola superiore, indicato come secondo assioma
della retta: “ogni punto di una retta la divide in due parti dette
semirette e il punto in questione si dice origine”. Chiaramente questo
va bene per l’idea che abbiamo di retta, ma va benissimo, per
esempio, anche per una circonferenza... Di qui infatti l’idea della
geometria proiettiva, nella quale, però due rette in un piano hanno
sempre un punto in comune. Si capisce meglio la geometria proiettiva se
la si immerge nel piano euclideo ampliato con la retta impropria,
costituito dal punto all’infinito (la direzione) del fascio di rette
parallele ad una data. Quindi due rette parallele hanno sempre un punto
(improprio) in comune, anzi, in un processo tipico della Matematica, si
può capovolgere quest’assunto facendolo diventare una definizione nella
geometria proiettiva.
Tutto ciò è stato premesso per esprimere, con esempi, come per capire
gli oggetti della Matematica si abbia bisogno di vari punti di vista
o rappresentazioni mentali, l’equivalente del riconoscere il cavallo
pur guardandolo da diversi punti di vista.
Qualche altra considerazione: si conosce un numero reale? Se si dovesse
farne un discorso di pura teoria dell’informazione, secondo Gregory
Chaitin non vi è nulla di più inconoscibile, perché, escluso il caso
particolare di un numero algebrico, per cui è pensabile una costruzione
con riga e compasso, il numero di byte necessario per esprimere un
numero reale è necessariamente infinito, anzi l’unica possibilità per
avere una serie di numeri interi completamente casuale è, secondo il
nostro, quella di scrivere in successione le cifre della
rappresentazione decimale di un numero reale.
Purtuttavia parecchi di noi hanno la percezione (presunzione?) di capire
i numeri reali. Da che cosa traiamo questa percezione? Da una parte
viene in soccorso l’algebra con la costruzione dei numeri reali a
partire dalla teoria assiomatica di Peano dei naturali, poi degli interi
e dei razionali con le usuali relazioni di equivalenza su NxN
e ZxZ, rispettivamente, ed infine con il passaggio ad R,
con le sezioni di Dedekind, semirette di Russell o completamento alla
Cauchy. Da un altro lato abbiamo la teoria assiomatica, la quale con i
nove assiomi sulle operazioni, i due sull’ordinamento (totale) e quello
sulla completezza garantisce che un corpo siffatto è unico a meno di
isomorfismi. Da un altro lato ancora la geometria analitica con
l’identificazione con una retta fornisce un’ulteriore utile
rappresentazione. Ma davvero si può dire di capire i numeri reali,
soprattutto con la premessa delle idee di Chaitin? Fuor di metafora:
davvero siamo in grado di fornire tutte le rappresentazioni possibili di
numeri reali? Sicuramente da questa mia disamina resta fuori la
rappresentazione dell’analisi non standard, ma quante altre ne esistono?
Esempio: che cosa rappresenta la figura qui sotto?
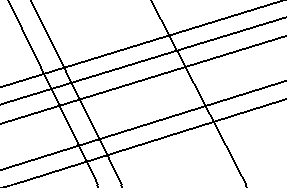
Pochi di noi riconosceranno il prodotto 32 x 21, ma
questa figura si presta a una rappresentazione e ad un calcolo veloce
per quella operazione.
Probabilmente la massima: “Più studio la Matematica, meno la capisco”,
allude al fatto che più si avanza nella conoscenza nel campo della
Matematica, tanto più si collezionano rappresentazioni mentali di un
dato concetto, fino a percepire che ci sarà sempre qualcosa che sfugge,
cioè più rappresentazioni mancanti, punti di vista diversi da infinite
possibili angolazioni.
Per “capire meglio il capire”, facciamo un giochino di
rappresentazione mentale. Naturalmente dovremo fare alcune assunzioni
che potrebbero risultare arbitrarie, ma, dopotutto, è solo un
giochino...
Immaginiamo che il contenuto di informazione di un ente o un gruppo di
enti matematici sia finito e di poter rappresentare questo contenuto con
un’area di una figura piana. Un triangolo equilatero, per semplicità,
andrà benissimo. Nel caso in cui la quantità di informazione sia
infinita, il discorso si potrebbe adattare a tutto il piano. A causa del
secondo teorema di Gödel, così come immaginato da Hofstadter, possiamo
immaginare che la ricerca di teoremi concernenti l’oggetto si dirami a
frattale nel nostro triangolo. Un frattale come la famosa felce andrà
benissimo. Immaginiamo che un punto di partenza per la costruzione del
frattale rappresenti un punto di vista particolare da cui partire per
dimostrare teoremi circa la classe di oggetti. Data l’obbligata
finitezza dei punti di vista (abbiamo solo risorse di spazio e di tempo
finite), la domanda è: da un numero finito di diversi punti di vista è
possibile cogliere tutte le sfaccettature (cioè capire) della teoria?
Traducendo questa domanda nella nostra rappresentazione abbiamo: è
possibile con un numero finito di frattali ricoprire tutto il triangolo?

Naturalmente, e questo è il bello della Matematica, ammesso che questa
mia “visione” sia significativa, fa sorgere mille altre domande.
Esempio: è possibile calcolare con la dimensione del frattale verità
dimostrabili? Se sì, la risposta alla domanda di sopra non dipenderà
sensibilmente dalla dimensione di questo frattale? È possibile che ci
sia un intervallo dimensionale in cui la risposta non è calcolabile (se
tutto questo ha un senso il dio burlone della matematica sicuramente
avrà predisposto così le
cose)? Naturalmente le mie domande riguardo ai frattali hanno una
valenza scientifica a prescindere dalla rappresentazione che se ne vuole
dare. Un poligono è ricopribile con un numero finito di frattali?
Dipende dalla dimensione dei frattali? Una risposta è data dalla curva
di Peano! Le altre credo siano aperte.
 Tutto questo naturalmente non può e non deve farci dimenticare il nostro
ruolo di insegnanti. Quali sono le ricadute di queste argomentazioni
sulle normali attività didattiche? La metariflessione che abbiamo
condotto sul significato di comprensione dà luogo ad alcune
considerazioni sul modo di far didattica. A prescindere dalla
metodologia usata, inquiry- based learning, costruttivismo, problem
solving, apprendimento collaborativo ed altro, bisogna comunque abituare
i nostri allievi a considerare molteplici punti di vista per focalizzare
i vari concetti, magari riprendendoli alla luce di nuovi fatti e
acquisizioni, realizzando il famoso processo a spirale evitando che
collassi in un cerchio, peggio, in un punto. Per fare questo,
naturalmente sembra necessario individuare dei nuclei fondamentali nella
disciplina senza pretesa di esaustività, lasciando alla libera
intrapresa dei nostri studenti l’eventuale minuzioso completamento
dei contenuti ritenuti non essenziali.
(Realizzazioni grafiche a cura di Ivana Niccolai)
Biblio- sitografia
http://video.google.it/videoplay?docid=4009629064835928534&q=moltiplicazione&total=164&start=10&num=10&so=0&type=search&plindex=9
Douglas R. Hofstadter- Gödel,
Escher, Bach:
un’Eterna
Ghirlanda Brillante.
Adelphi 1992 Milano
Benoît B. Mandelbrot Gli oggetti frattali
Forma, caso e
dimensione. Einaudi
1987 Torino
Gregory J. Chaitin Casualità e dimostrazione matematica. Le Scienze
Settembre 1975
Carl B. Boyer Storia della Matematica Mondadori 1998 Milano |