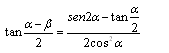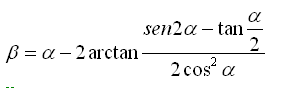"Vorrei proporvi un gioco geometrico che ho
scoperto per caso.
Dapprima vi descrivo questo gioco: cinque punti (A,
B, C, D ed E) sono disposti sul piano in una particolare
configurazione:
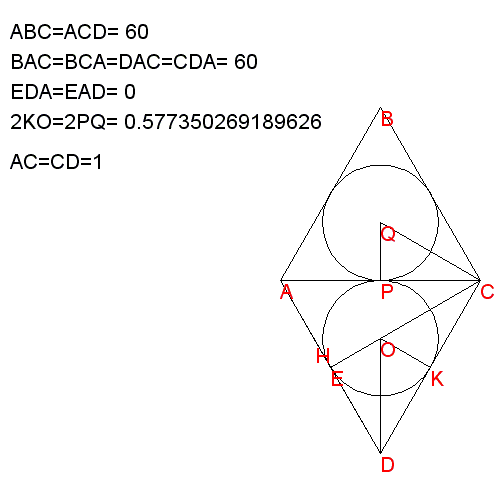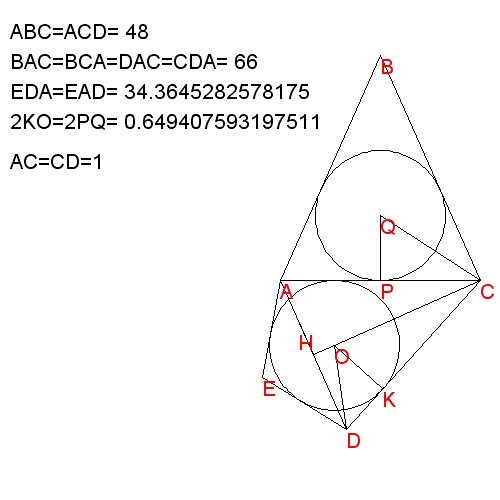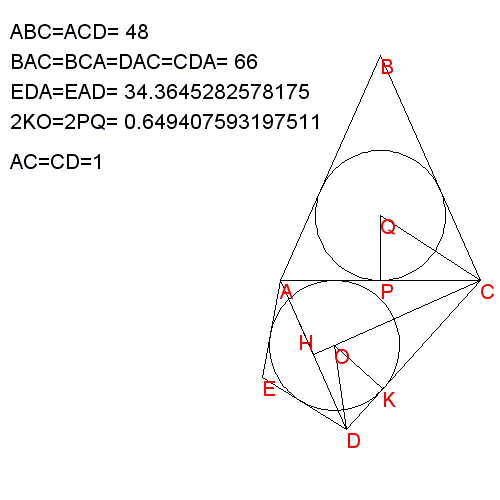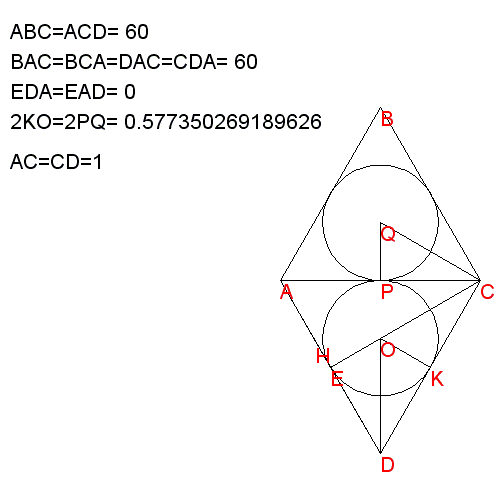
| ABC è un triangolo
isoscele L'angolo in A è uguale e 64° L'angolo in B è uguale e 52° L'angolo in C è uguale e 64° |
ACD è un triangolo
isoscele L'angolo in A è uguale e 64° L'angolo in C è uguale e 52° L'angolo in D è uguale e 64° |
ADE è un triangolo
isoscele L'angolo in A è uguale e 18° L'angolo in D è uguale e 18° L'angolo in E è uguale e 144° |
Il lato AC misura 1,0000
m
Chiederei:
1) Quanto misura il diametro del
cerchio iscritto nel triangolo ABC?
2) Quanto misura il
diametro del cerchio iscritto nel deltoide ACDE?
Ho provato a
disegnare su un foglio abbastanza esteso questo triangolo isoscele ABC
saldato al deltoide ACDE e i due cerchi sembrano
«particolarmente
uguali». Si può ottenerne una conferma?
In più, sarebbe possibile
creare altre configurazioni legate a quella da me proposta e valutare se i
due cerchi iscritti (nel triangolo ABC e nel deltoide ACDE) sono
uguali?
Mi spiego: ancora lavorando con i tre triangoli isosceli ABC,
ACD e ADE con il lato AC in comune tra il triangolo ABC e il deltoide ACDE
è possibile creare un'altra configurazione di questi punti dove sia
possibile variare l'ampiezza degli angoli, tenendoli assolutamente interi
(ovvero gli angoli non dovrebbero presentare decimali), per raggiungere i
due cerchi iscritti d'uguale diametro?
Se ad esempio imponessi l'angolo in A di ABC a
48° (gli altri in ABC evidentemente sarebbero entrambi a 66°) così come
l'angolo in C di ACD, sarebbe possibile giocare con gli angoli del
triangolo ADE per permettere di iscrivere perfettamente nel deltoide il
cerchio iscritto in ABC?
Tutto questo per rincuorarmi sul fatto che non
solo unicamente con gli angoli della mia iniziale configurazione sia
possibile ottenere uguali i due
cerchi iscrivibili!"
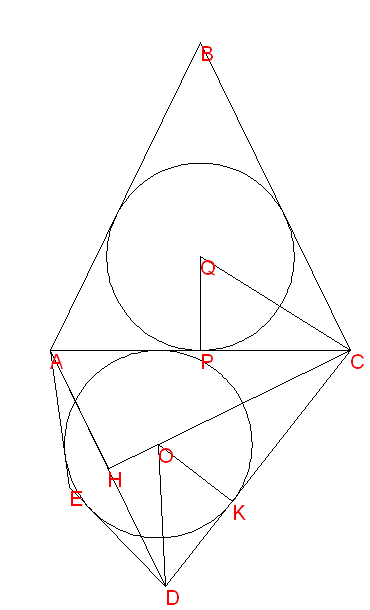 |
AC=CD=1
BAC=BCA=CAD=ADC=64
ABC=ACD=52
AED=144 EAD=ADE=18 Q è intersezione delle
bisettrici del triangolo ABC
PC=1/2=0.5
PCQ=64/2=32
PQ/PC=tanPCQ
PQ=0.5*tan32 -primo raggio O è intersezione delle
bisettrici del deltoide ACDE
AH/AC=cosCAD
HC/AC=senCAD
ma AC=1 CAD=64
dunque
AH=cos64=HD HC=sen64 EDC=CAD+EDA
EDC=64+18=82
EDO=EDC/2
EDO=41 HDO=EDO-EDA
HDO=41-18=23 OH/HD=tanHDO
OH=(tan23)*(cos64)
OC=CH-OH
OC=sen64-cos64*tan23 essendo il triangolo OKC
simile a ACH
OK/AH=OC/AC
OK/cos64=OC/1
OK=OC*cos64
sostituendo
OK=(sen64-cos64*tan23)*cos64
- secondo raggio
| ||||||||||||
| Dunque il diametro iscritto del cerchio inscritto in ABC
essendo doppio del raggio PQ è tan32=0.624869351909328 mentre il diametro del cerchio inscritto nel deltoide è il doppio di OK: 2(cos 64)(sin 64)-(cos 64)*(tan 23)= 0.62486872898331 Come si vede i due valori, pur essendo vicini, non coincidono. La loro differenza non è zero ma 0.000000622926017213032. | |||||||||||||
| Essendo i cerchi disuguali non si può quindi trovare la conferma richiesta. | |||||||||||||
Ponendo ora a=64 si
ottiene b=18.0001573720485 il che conferma come
non ci sia predilezione per gli angoli interi. La vicinanza a 18
appare solo come una accidentale coincidenza.
L'animazione mostra, infine, cosa succede al variare dei possibili valori interi di BAC=a .
| |||||||||||||